STATISTICS PROBLEMS WITH SOLUTIONS FOR GRADE 10

Problem 1 :

The frequency distribution is given below.

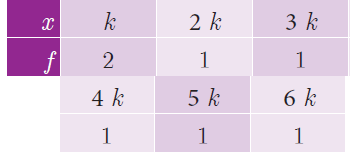
In the table, k is a positive integer, has a variance of 160. Determine the value of k.

Solution :

Variance  =  (Σfd²/Σf) - (Σfd/Σf)²

d = x - A (A = 3k)

Σfd  =  -5k + k + 2k + 3k 

Σfd  =  k

Σfd²  =  23k² and Σf  =  7

Variance  =  (23k²/7) - (k/7)²

  =  (161k² - 1k²)/49

  =  160k²/49

160k²/49  =  160

k²/49  =  1

k²  =  49

k = 7

Problem 2 :

The standard deviation of some temperature data in degree celsius (^oC) is 5. If the data were converted into degree Farenheit (^oF) then what is the variance?

Solution :

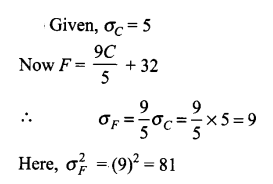
Problem 3 :

If for a distribution, Σ(x −5) = 3, Σ(x −5)² = 43,and total number of observations is 18, find the mean and standard deviation

Solution :

Σ(x −5) = 3

Σx − Σ5 = 3

Σx − 18(5) = 3

Σx  = 90 + 3  ==>  93

Σ(x −5)² = 43

Σ(x² - 10x + 5²) = 43

Σ(x² - 10x + 25) = 43

Σx² - 10Σx + 25Σ = 43

Σx² - 10(93) + 25(18) = 43

Σx²  = 43 + 930 - 450 

Σx²  = 523

Mean :

  =  Σx/n  =  93/18  =  5.17

Standard deviation :

√(Σx²/n) -⁽Σx/n)²  

  =  √(523/18) - (5.17)²

  =  √29.05 - 26.72

  =  √2.33

S.D  =  1.53

Problem 4 :

Prices of peanut packets in various places of two cities are given below. In which city, prices were more stable?

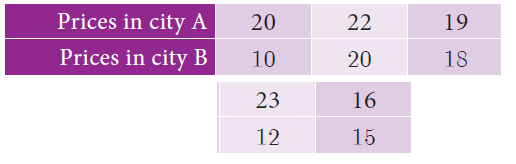
Solution :

By finding the coefficient of variation, we come to know that which is more stable.

Standard deviation :

σ  =  √(Σx²/n) -⁽Σx/n)²  

For city A :

σ  =  √(Σx²/n) -⁽Σx/n)²  

  =  √(2030/5) -(100/5)²  

  =  √406 - 400

  =  √6

  =  2.44

Coefficient of variation  =  (σ/x̄) x 100%

=  (2.44/20) x  100%

=  12.2

For city B :

σ  =  √(Σx²/n) -⁽Σx/n)²  

  =  √(1193/5) -(75/5)²  

  =  √238.6 - 225

  =  √13.6

  =  3.68

Coefficient of variation  =  (σ/x̄) x 100%

=  (3.68/15) x  100%

=  24.53

So, in city A, prices are more stable.

Problem 5 :

If the range and coefficient of range of the data are 20 and 0.2 respectively, then find the largest and smallest values of the data.

Solution :

Range  =  L - S  =  20  ---(1)

Coefficient of range  =  (L - S)/(L + S)  =  0.2

20/(L + S)  =  0.2

L + S  =  20/0.2

L + S  =  100 ---(2)

(1) + (2)

2L  =  120

L  =  60

By applying the value of L, we get 

S  =  100 - 60

S  =  40

So, the largest and smallest values are 60 and 40 respectively.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.