SUM OF ALL 3 DIGIT NUMBERS DIVISIBLE BY 6

To get the sum of 3 digit numbers divisible by 6, first we have to find the first and last 3 digit numbers divisible by 6.

First 3 Digit Number Exactly  Divisible by 6

The first and also the smallest 3 digit number is 100.

To find the first 3 digit number divisible by 6, we have to divide the very first 3 digit number 100 by 6 

100/6  =  16.67

We have decimal in the result of 100/6.

Clearly the first 3 digit number 100 is not exactly divisible by 6

Let us divide the second 3 digit number 101 by 6

101/6  =  16.83

We have decimal in the result of 101/6 also.

So, the second 3 digit number 101 is also not exactly divisible by 6

Here, students may have some questions on the above process.

They are,

1. Do we have to divide the 3 digit numbers by 6 starting from 100 until we get a 3 digit number which is exactly divisible by 6 ?

2. Will it not take a long process ?

3. Is there any shortcut instead of dividing the 3 digit numbers 100, 101, 102.... one by one ?

There is only one answer for all the above three questions.

That is, there is a shortcut to find the first three digit number which is exactly divisible by 6.

SHORTCUT

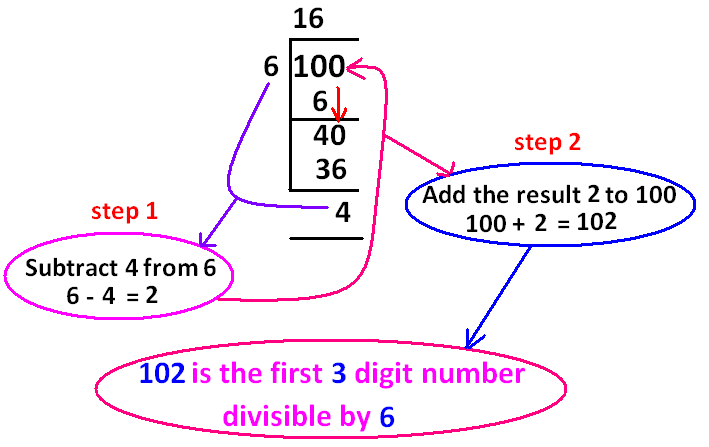
What has been done in the above shortcut ?

The process which has been done in the above shortcut has been explained clearly in the following steps.

Step 1 :

To get the first 3 digit number divisible by 6, we have to take the very first 3 digit number 100 and divide it by 6. 

Step 2 :

When we divide 100 by 6 using long division as given above, we get the remainder 4. 

Step 3 :

Now, the remainder 4 has to be subtracted from the divisor 6.

When we subtract the remainder 4 from the divisor 6, we get the result 2 (That is 6 - 4 = 2).

Step 4 :

Now, the result 2 in step 3 to be added to the dividend 100. 

When we add 2 to 100, we get 102

Now, the process is over. 

So, 102 is the first 3 digit number exactly divisible by 6

This is how we have to find the first 3 digit number exactly divisible by 6

Important Note :

This method is not only applicable to find the first 3 digit number exactly divisible by 6. It can be applied to find the first 3 digit number exactly divisible by any number, say k.

Last 3 Digit Number Exactly  Divisible by 6

The last and also the largest 3 digit number is 999.

To find the last 3 digit number divisible by 6, we divide the very last  3 digit number 999 by 6. 

999/6  =  166.5

We have decimal in the result of 999/6.

Clearly the last 3 digit number 999 is not exactly divisible by 6.

Let us divide the preceding 3 digit number 998 by 6.

998/6 = 166.33

We have decimal in the result of 998/6 also.

So, the preceding 3 digit number 998 also is not exactly divisible by 6

Here, students may have some questions on the above process.

They are,

1. Do we have to divide the 3 digit numbers .........997, 998, 999 by 6 until we get a 3 digit number which is exactly divisible by 6 ?

2. Will it not take a long process ?

3. Is there any shortcut instead of dividing the 3 digit numbers ...........997, 998, 999 one by one ?

There is only one answer for all the above three questions.

That is, there is a shortcut to find the last three digit number which is exactly divisible by 6.

SHORTCUT

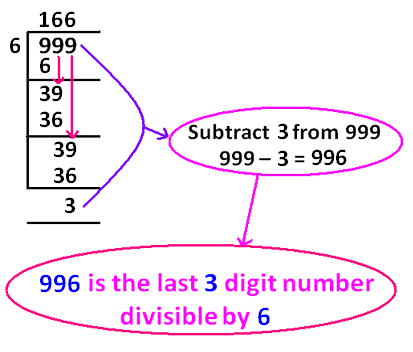
What has been done in the above shortcut ?

The process which has been done in the above shortcut has been explained clearly in the following steps.

Step 1 :

To get the last 3 digit number divisible by 6, we have to take the very last 3 digit number 999 and divide it by 6. 

Step 2 :

When we divide 999 by 6 using long division as given above, we get the remainder 3. 

Step 3 :

Now, the remainder 3 has to be subtracted from the dividend 999.

When we subtract the remainder 3 from the dividend 999, we get the result 996 (That is 999 - 3  =  996).

Now, the process is over. 

So, 996 is the last 3 digit number exactly divisible by 6.

This is how we have to find the last 3 digit number exactly divisible by 6.

Important Note :

The process of finding the first 3 digit number exactly divisible by 6 and the process of finding the last 3 digit number exactly divisible by 6 are completely different.

Be careful! Both are not same.

The methods explained above are not only applicable to find the first 3 digit number and last 3 digit number exactly divisible by 6. They can be applied to find the first 3 digit number and last 3 digit number exactly divisible by any number, say k.

Sum of all 3 Digit Numbers Divisible by 6

Let us see how to find the sum of all 3 digit numbers divisible by 6 in the following steps.

Step 1 :

The first 3 digit number divisible by 6 is 102.

After 102, to find the next 3 digit number divisible by 6, we have to add 6 to 102. So the second 3 digit number divisible by 6 is 108.

In this way, to get the succeeding 3 digit numbers divisible by 6, we just have to add 6 as given below. 

102, 108, 114, 120,.......................996

Clearly, the above sequence of 3 digit numbers divisible by 6 forms an arithmetic sequence. 

And our aim is to find the sum of the terms in the above arithmetic sequence.  

Step 2 :

In the arithmetic sequence

102, 108, 114, 120,.......................996

we have

first term  =  102

common difference  =  6

last term  =  996

That is,

a  =  102

d  =  6

l  =  996

Step 3 :

The formula to find the numbers of terms in an arithmetic sequence is given by

n = [(l - a) / d] + 1

Substitute a = 102, l = 996 and d = 6.

n  =  [(996 - 102) / 6] + 1

n  =  [894/6] + 1 

n  =  149 + 1

n  =  150

So, number of 3 digit numbers divisible by 6 is 150.

Step 4 :

The formula to find the sum of 'n' terms in an arithmetic sequence is given by

=  (n/2)(a + l)

Substitute a = 102, d = 6, l = 996 and n = 150.

=  (150/2)(102 + 996)

=  75 x 1098

=  82350

So, the sum of all 3 digit numbers divisible by 6 is 82350.

Note :

The method explained above is not only applicable to find the sum of all 3 digit numbers divisible by 6. This same method can be applied to find sum of all 3 digit numbers divisible by any number, say k.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.