SUM OF ALL 3 DIGIT NUMBERS DIVISIBLE BY 7

To get the sum of 3 digit numbers divisible by 7, first we have to find the first and last 3 digit numbers divisible by 7. 

First 3 Digit Number Exactly  Divisible by 7

The first and also the smallest 3 digit number is 100.

To find the first 3 digit number divisible by 7, we divide the very first 3 digit number 100 by 7 

100/7  =  14.29

We have decimal in the result of 100/7.

Clearly the first 3 digit number 100 is not exactly divisible by 7.

Let us divide the second 3 digit number 101 by 7.

101/7  =  14.43

We have decimal in the result of 101/7 also.

So, the second 3 digit number 101 is also not exactly divisible by 7

Here, students may have some questions on the above process.

They are,

1. Do we have to divide the 3 digit numbers by 7 starting from 100 until we get a 3 digit number which is exactly divisible by 7?

2. Will it not take a long process?

3. Is there any shortcut instead of dividing the 3 digit numbers 100, 101, 102.... one by one?

There is only one answer for all the above three questions.

That is, there is a shortcut to find the first three digit number which is exactly divisible by 7.

SHORTCUT

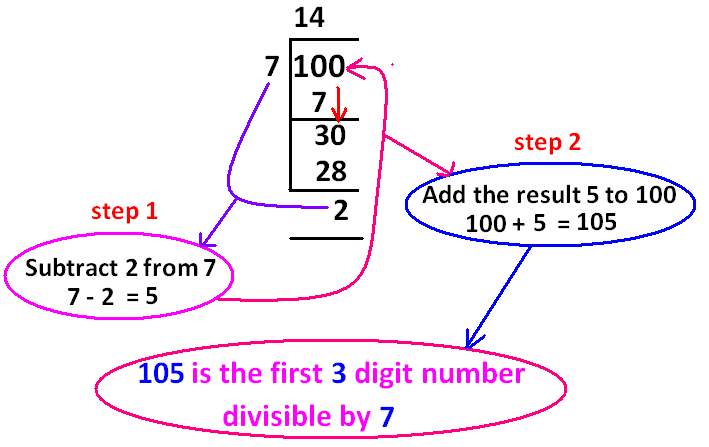
What has been done in the above shortcut ?

The process which has been done in the above shortcut has been explained clearly in the following steps.

Step 1 :

To get the first 3 digit number divisible by 7, we have to take the very first 3 digit number 100 and divide it by 7. 

Step 2 :

When we divide 100 by 7 using long division as given above, we get the remainder 2. 

Step 3 :

Now, the remainder 2 has to be subtracted from the divisor 7.

When we subtract the remainder 2 from the divisor 7, we get the result 5 (That is 7 - 2 = 5).

Step 4 :

Now, the result 5 in step 3 to be added to the dividend 100. 

When we add 5 to 100, we get 105.

Now, the process is over. 

So, 105 is the first 3 digit number exactly divisible by 7.

This is how we have to find the first 3 digit number exactly divisible by 7.

Important Note :

This method is not only applicable to find the first 3 digit number exactly divisible by 7. It can be applied to find the first 3 digit number exactly divisible by any number, say k.

Last 3 Digit Number Exactly  Divisible by 7

The last and also the largest 3 digit number is 999.

To find the last 3 digit number divisible by 7, we divide the very last  3 digit number 999 by 7. 

999/7  =  142.71

We have decimal in the result of 999/7

Clearly the last 3 digit number 999 is not exactly divisible by 7.

Let us divide the preceding 3 digit number 998 by 7.

998/7  =  142.57

We have decimal in the result of 998/7 also.

So, the preceding 3 digit number 998 also is not exactly divisible by 7

Here, students may have some questions on the above process.

They are,

1. Do we have to divide the 3 digit numbers .......997, 998, 999 by 7  until we get a 3 digit number which is exactly divisible by 7 ?

2. Will it not take a long process ?

3. Is there any shortcut instead of dividing the 3 digit numbers ...........997, 998, 999 one by one ?

There is only one answer for all the above three questions.

That is, there is a shortcut to find the last three digit number which is exactly divisible by 7.

SHORTCUT

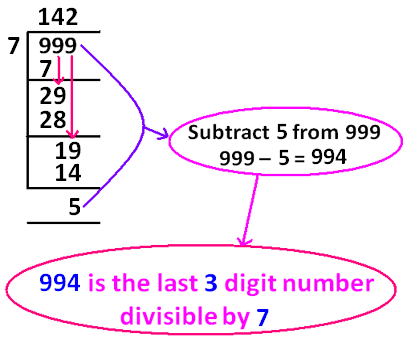
What has been done in the above shortcut ?

The process which has been done in the above shortcut has been explained clearly in the following steps.

Step 1 :

To get the last 3 digit number divisible by 7, we have to take the very last 3 digit number 999 and divide it by 7. 

Step 2 :

When we divide 999 by 7 using long division as given above, we get the remainder 5. 

Step 3 :

Now, the remainder 5 has to be subtracted from the dividend 999.

When we subtract the remainder 5 from the dividend 999, we get the result 994 (That is 999 - 5 = 994).

Now, the process is over. 

So, 994 is the last 3 digit number exactly divisible by 7.

This is how we have to find the last 3 digit number exactly divisible by 7.

Important Note :

The process of finding the first 3 digit number exactly divisible by 7 and the process of finding the last 3 digit number exactly divisible by 7 are completely different.

Be careful! Both are not same.

The methods explained above are not only applicable to find the first 3 digit number and last 3 digit number exactly divisible by 7. They can be applied to find the first 3 digit number and last 3 digit number exactly divisible by any number, say k.

Sum of All 3 Digit Numbers Divisible by 7

Let us see how to find the sum of all 3 digit numbers divisible by 7 in the following steps.

Step 1 :

The first 3 digit number divisible by 7 is 105.

After 105, to find the next 3 digit number divisible by 7, we have to add 7 to 105. So the second 3 digit number divisible by 7 is 112.

In this way, to get the succeeding 3 digit numbers divisible by 7, we just have to add 7 as given below. 

105, 112, 119, 126,...................994

Clearly, the above sequence of 3 digit numbers divisible by 7 forms an arithmetic sequence. 

And our aim is to find the sum of the terms in the above arithmetic sequence. 

Step 2 :

In the arithmetic sequence

105, 112, 119, 126,...................994, 

we have

first term  =  105

common difference  =  7

last term  =  994

That is,

a  =  105

d  =  7

l  =  994

Step 3 :

The formula to find the numbers of terms in an arithmetic sequence is given by

n = [(l - a) / d] + 1

Substitute a = 105, l = 994 and d = 7.

n  =  [(994 - 105) / 7] + 1

n  =  [889/7] + 1

n  =  127 + 1

n  =  128

So, number of 3 digit numbers divisible by 7 is 128.

Step 4 :

The formula to find the sum of n terms in an arithmetic sequence is given by

=  (n/2)(a + l)

Substitute a = 105, d = 7, l = 994 and n = 128.

=  (128/2)(105 + 994)

=  64 x 1099

=  70336

So, the sum of all 3 digit numbers divisible by 7 is 70336.

Note :

The method explained above is not only applicable to find the sum of all 3 digit numbers divisible by 7. This same method can be applied to find sum of all 3 digit numbers divisible by any number, say k.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.