SUM OF ARITHMETIC GEOMETRIC AND ARITHMETICO GEOMETRIC SEQUENCES

Here we are going to see some practice questions on finding sum of arithmetic geometric and arithmetico geometric sequences.

Question 1 :

Find the sum of the first 20-terms of the arithmetic progression having the sum of first 10 terms as 52 and the sum of the first 15 terms as 77

Solution :

S₁₅  =  77

S_n  =  (n/2)[2a + (n - 1)d]

S₁₀  =  52

S₁₀ = 52 = (10/2)[2a + 9d]

52  =  10a + 45d  ---------(1)

S₁₅  =  77

S₁₅ = 77 = (15/2)[2a + 14d]

77  =  15a + 105d  ---------(2)

(1) ⋅ 3 ==> 30a + 135 d  =  156

(2) ⋅ 2 ==> 30a + 210 d  =  154

                 (-)     (-)         (-)

              -----------------------

                        -75d  =  2  ==> d  =  -2/75

By applying the value of d in (1), we get

10 a + 45 (-2/75)  =  52

10a - 6/5  =  52

10a  =  52 + (6/5)  ==> 10a  =  266/5

 a  =  266/50  ==>  133/25

Sum of arithmetic series :

S_n  =  (n/2)[2a + (n - 1)d]

S₂₀  =  (20/2)[2(133/25) + (20 - 1)(-2/75)]

  =  10[266/25 + 19(-2/75)]

  =  10[(266/25) - (38/75)]

  =  10[(798 - 38)/75]

  S₂₀  =  10(760/75)  =  10(152/15)  ==> 304/3

Question 2 :

Find the sum up to the 17th term of the series

(1³/1 ) + (1³ + 2³) / (1 + 3) + (1³ + 2³ + 3³) / (1 + 3 + 5) + · · ·

Solution :

First let us find the nth term of the sequence

In the numerator, we have sum of cubes of natural numbers.

In the denominator, we have sum of odd numbers

n^th term  t_n = (1³+2³+3³+ .............+ n³)/(1+3+5+ ...+ (2n - 1))

t_n  =  [n(n+1)/2]²/n²

  =  (n+1)²/4

  =  (1/4)[n² + 2n + 1]

Let Sn denote the sum of n terms of the given series. Then

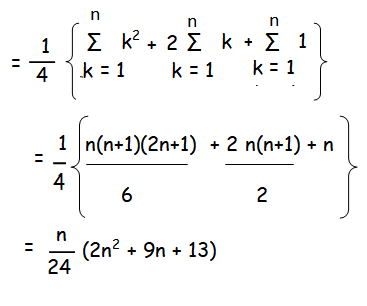
n = 17

  =  17/24 (578 + 153 + 13)

  =  (17/24)(744)

  =  17 (31)  =  527

Hence the sum of 17 terms of the given sequence is 527.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.