SUM OF EXTERIOR ANGLES OF A POLYGON WORKSHEET

Problem 1 :

Find the measure of each exterior angle of a regular decagon. 

Problem 2 :

If the measure of each exterior angle of a regular pentagon is (2x + 4)°, find the value of x. 

Problem 3 :

Find the measure of each exterior angle of the regular polygon given below. 

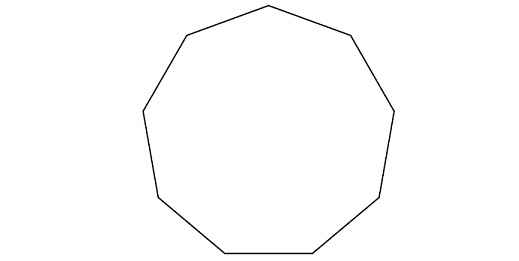
Problem 4 :

Find the measure of exterior angle corresponding to the interior angle x° in the irregular polygon given below. 

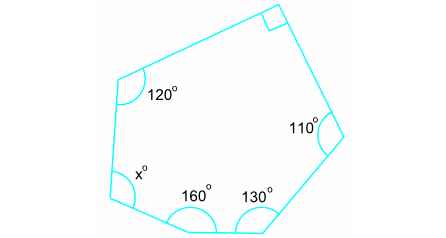
Problem 5 :

In a polygon, the measure of each interior angle is (5x + 90)° and exterior angle is (3x - 6)°. How many sides does the polygon have ?

1. Answer :

Decagon is a 10-sided polygon.

In any polygon, the sum of exterior angles is 

=  360°

Formula to find the measure of each exterior angle of a regular n-sided polygon is :

360°/n

Then, we have 

=  360°/10

=  36°

So, the measure of each exterior angle of a regular decagon is 36°. 

2. Answer :

Pentagon is a 5-sided polygon.

In any polygon, the sum of exterior angles is 

=  360°

Formula to find the measure of each exterior angle of a regular n-sided polygon is :

360°/n

Then, we have 

=  360°/5

=  72°

The measure of each exterior angle is 72°. 

Given : The measure of each exterior angle of a regular pentagon is (2x + 4)°. 

So, we have 

(2x + 4)°  =  72°

2x + 4  =  72

Subtract 4 from both sides.  

2x  =  68 

Divide both sides by 

x  =  34

So, the value of x is 34. 

3. Answer :

Let us count the number of sides of the polygon given above. 

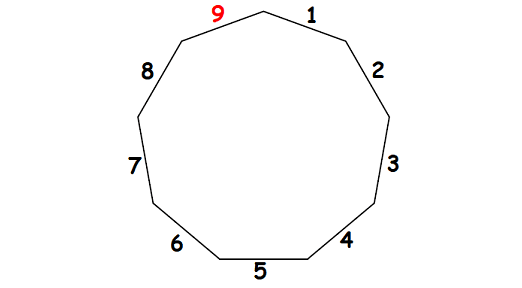
So, the above regular polygon has 9 sides. 

In any polygon, the sum of exterior angles is 

=  360°

Formula to find the measure of each exterior angle of a regular n-sided polygon is :

360°/n

Then, we have 

=  360°/9

=  40°

So, the measure of each exterior angle of a regular polygon is 40°. 

4. Answer :

To find the measure of exterior angle corresponding to x° in the above polygon, first we have to find the value of x. 

The above diagram is an irregular polygon of 6 sides (Hexagon) with one of the interior angles as right angle. 

Formula to find the sum of interior angles of a n-sided polygon is 

=  (n - 2) ⋅ 180°

By using the formula,  sum of the interior angles of the above polygon is 

=  (6 - 2) ⋅ 180°

=  4 ⋅ 180°

=  720° ------(1)

By using the angles, sum of the interior angles of the above polygon is  

=  120° + 90° + 110° + 130° + 160 + x°

=  610° + x° ------(2)

From (1) and (2), we get

610° + x°  =  720°

610 + x  =  720

Subtract 610 from both sides. 

x  =  110

So, the measure of interior angle represented by x is 110°.

In any polygon, the sum of an interior angle and its corresponding exterior angle is 180°.

That is,

Interior angle + Exterior Angle  =  180°

Then, we have

x° + Exterior Angle  =  180°

110° + Exterior angle  =  180°

Exterior angle  =  70°

So, the measure of each exterior angle corresponding to x° in the above polygon is 70°. 

5. Answer :

In any polygon, the sum of an interior angle and its corresponding exterior angle is 180°.

That is,

Interior angle + Exterior Angle  =  180°

(5x + 90)° + (3x - 6)°  =  180°

5x + 90 + 3x - 6  =  180

8x + 84  =  180

8x  =  96

x  =  12

Finding the measure of exterior angle :

Exterior angle  =  (3x-6)°

Exterior angle  =  (3 ⋅ 12 - 6)°

Exterior angle  =  (36 - 6)°

Exterior angle  =  30°

Formula to find the number of sides of a regular polygon is

=  360 / Measure of each exterior angle 

Then, we have

=  360 / 30

=  12

So, the given polygon has 12 sides. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.