SUM OF N TERMS OF SERIES

Question 1 :

Find the general term and sum to n terms of the sequence

1, 4/3 , 7/9 , 10/27, . . . .

Solution :

1, 4/3 , 7/9 , 10/27, . . . .

a = 1, d = 3, r = 1/3

General term :

t_n  =  ((a + (n − 1)d)rⁿ⁻¹)

t_n  =  ((1 + (n − 1)3)(1/3)ⁿ⁻¹)

  =  (1 + 3n - 3)(1/3)ⁿ⁻¹

t_n  =  (3n - 2)/3^{n −1}

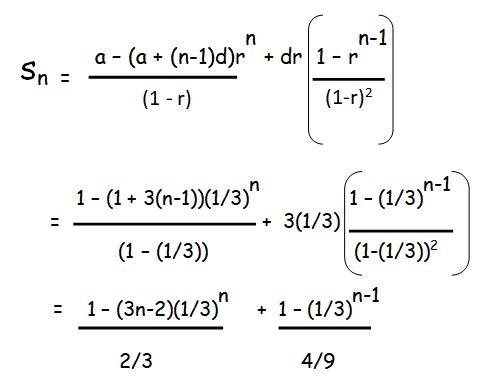
S_n  =  3ⁿ - (3n - 2)/2⋅3^n-1 + (3^n-1 - 1)/(8 ⋅ 3^n-3)

Question 2 :

Find the value of n, if the sum to n terms of the series

√3 + √75 + √243 + · · · is 435√3.

Solution :

√3 + √75 + √243 + · · ·+ n terms

√3 + 5√3 + 9√3 + · · ·+ n terms

The given series is arithmetic series.

S_n  =  435√3

(n/2)[2a+ (n-1)d]  = 435√3

a = √3, d = 4√3

(n/2)[2√3+ (n-1)(4√3)]  = 435√3

(n/2)[2√3+ 4√3n - 4√3)]  = 435√3

(n/2)[4√3n - 2√3)]  = 435√3

n[2√3n - √3]  = 435√3

Divide by √3 on both sides

n[2n - 1]  = 435

2n² - n - 435  =  0

(n - 15) (2n + 29)  =  0

n = 15, n = -29/2

Hence the value of n is 15.

Question 3 :

Show that the sum of (m + n)^th and (m − n)^th term of an AP. is equal to twice the m^th term

Solution :

t_m+n  =  a + (m + n - 1)d  ------(1)

t_m-n  =  a + (m - n - 1)d  ------(2)

(1) + (2)  

t_m+n + t_m-n  =  a + (m + n - 1)d + a + (m - n - 1)d 

  =  a + md + nd - d + a + md - nd - d 

  =  2a + 2md - 2d

  =  2 [a + (m-1) d]

  =  2 t_m

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.