SURDS AND INDICES

Surds

Let a be a rational number and n be a positive integer such that 

a^1/n  =  ⁿ√a

Then, ⁿ√a is called a surd of order n. 

Laws of Surds

Law 1 : 

ⁿ√a  =  a^1/n

Law 2 : 

ⁿ√(ab)  =  ⁿ√a x ⁿ√b

Law 3 : 

ⁿ√(a/b)  =  ⁿ√a / ⁿ√b

Law 4 : 

(ⁿ√a)ⁿ  =  a

Law 5 : 

^m√(ⁿ√a)  =  ^mn√a

Law 6 : 

(ⁿ√a)^m  =  ⁿ√a^m

Laws of Indices

Law 1 : 

x^m ⋅ xⁿ  =  x^m+n

Law 2 : 

x^m ÷ xⁿ  =  x^m-n

Law 3 : 

(x^m)ⁿ  =  x^mn

Law 4 : 

(xy)^m  =  x^m ⋅ y^m

Law 5 : 

(x / y)^m  =  x^m / y^m

Law 6 : 

x^-m  =  1 / x^m

Law 7 : 

x⁰  =  1

Law 8 : 

x¹  =  x

Law 9 : 

x^m/n  =  y -----> x  =  y^n/m

Law 10 : 

(x / y)^-m  =  (y / x)^m

Law 11 : 

a^x  =  a^y -----> x  =  y

Law 12 : 

x^a  =  y^a -----> x  =  y

Practice Problems

Problem 1 : 

If x^1/p  =  y^1/q  =  z^1/r and xyz  =  1, then find  the value of
(p + q + r).  

Solution : 

Let  x^1/p  =  y^1/q  =  z^1/r  =  k.

Then,

x^1/p  =  k -----> x  =  k^p

y^1/q  =  k -----> y  =  k^pq

z^1/r  =  k -----> z  =  k^r

Given : xyz  =  1

Then,

xyz  =  1

k^p ⋅ k^q ⋅ k^r  =  1

k^{p + q + r}  =  1 -----(1)

We know that a⁰  =  1.

So,

k⁰ = 1

In (1),  substitute 1  =  k⁰.

(1) -----> k^{p + q + r}  =  k⁰

Using law 11 of indices, we get

p + q + r  =  0

Problem 2 : 

Simplify : 

[1-{1-(1-x²)^-1}^-1]^-1/2

Solution : 

[1-{1-(1-x²)^-1}^-1]^-1/2  :

=  [1-{1-1/(1-x²)}^-1]^-1/2

=  [1-{(1-x²-1)/(1-x²)}^-1]^-1/2

=  [1-{-x²/(1-x²)}^-1]^-1/2

=  [1-{x²/(x²-1)}^-1]^-1/2

=  [1-(x²-1)/x²]^-1/2

=  [{x²-(x²-1)}/x²]^-1/2

=  [(x²-x²+1)/x²]^-1/2

=  [1/x²]^-1/2

=  [x²]^1/2

=  x

Problem 3 : 

Using (a - b)³ = a³ - b³ - 3ab(a-b), if x  =  p^1/3 - p^-1/3, find the value of 

x³ + 3x

Solution : 

Given : x = p^1/3 - p^-1/3

Take power 3 on both the sides.

x³  =  (p^1/3 - p^-1/3)³

Using (a - b)³  =  a³ - b³ - 3ab(a - b).

x³  =  (p^1/3)³ - (p^-1/3)³ - 3p^1/3.p^-1/3(p^1/3-p^-1/3)

x³  =  p - p^-1 - 3p^{1/3 - 1/3}(x)

x³  =  p - 1/p - 3p⁰x

x³  =  p - 1/p - 3(1)x

x³  =  p - 1/p - 3x

x³ + 3x  =  p - 1/p

Problem 4 : 

Simplify : 

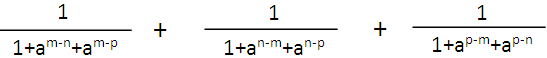
Solution : 

Problem 5 : 

If x  =  3^1/3 + 3^-1/3, find the value of 

3x³ - 9x

Solution : 

Given : x = 3^1/3 + 3^-1/3

Take power 3 on both the sides.

x³  =  (3^1/3 + 3^-1/3)³

Using (a + b)³  =  a³ + b³ + 3ab(a + b).

x³  =  (3^1/3)³ + (3^-1/3)³ + 3 ⋅ 3^1/3 ⋅ 3^-1/3(3^1/3 + 3^-1/3)

x³  =  3 + 3^-1 + 3 ⋅ 3^{1/3 - 1/3} ⋅x

x³  =  3 + 1/3 + 3 ⋅ 3⁰ ⋅ x

x³  =  3 + 1/3 + 3(1)x

x³  =  3 + 1/3 + 3x

x³ - 3x  =  3 + 1/3

Multiply each side by 3.

3(x³ - 3x)  =  3(3 + 1/3)

3x³ - 9x  =  9 + 1

3x³ - 9x  =  10

Problem 6 :

If a^x = b, b^y = c and  c^z = a, then find the value of xyz. 

Solution : 

Let

a^x  =  b -----(1)

b^y  =  c -----(2)

c^z  =  a -----(3)

Substitute a  =  c^z in (1).

(1)-----> (c^z)^x  =  b

c^zx  =  b

Substitute c  =  b^y.

(b^y)^zx  =  b

b^xyz  =  b

b^xyz  =  b¹

xyz  =  1

Problem 7 :

If  2^x  =  3^y  =  6^-z, then find the value of

1/x  +  1/y  +  1/z  

Solution : 

Let 2^x  =  3^y  =  6^-z  =  k.

Then, 

2^x  =  k ----->  2  =  k^1/x

3^y  =  k -----> 3  =  k^1/y

6^-z  =  k -----> 6  =  k^-1/z

And also, 

6  =  k^-1/z 

(2 x 3)  =  k^-1/z

In (1), substitute 2  =  k^1/x, 3  =  k^1/y_.

k^1/x ⋅ k^1/y  =  k^-1/z

k^{1/x + 1/y}  =  k^-1/z

Using law 11 of indices, we get

1/x + 1/y  =  -1/z

1/x + 1/y + 1/z  =  0

Problem 8 :

If (√9)^-7 ⋅ (√3)^-4  =  3^k, then find the value of k. 

Solution : 

(9^1/2)^-7 ⋅ (3^1/2)^-4  =  3^k

(9)^-7/2 ⋅ (3)^-4/2  =  3^k

(3²)^-7/2 ⋅ 3^-2  =  3^k

3^{2 ⋅ (-7/2)} ⋅ 3^-2  =  3^k

3^-7 ⋅ 3^-2  =  3^k

3^{-7 - 2}  =  3^k

3^-9  =  3^k

k  =  -9

So, the value of k is -9.

Problem 9 :

If √(x√x)   =  x^a, then find the value of a.

Solution : 

√(x√x)   =  x^a

√(x ⋅ x^1/2)   =  x^a

√(x^{1 + 1/2})   =  x^a

√(x^3/2)   =  x^a

(x^3/2)^1/2   =  x^a

x^3/4   =  x^a

3/4  =  a

So, the value of a is 3/4.

Problem 10 :

If n³   =  x, n⁴  =  20x and n > 0, then find the value of n. 

Solution : 

n⁴  =  20x

n³ ⋅ n  =  20x

Substitute x for n³.

  x ⋅ n  =  20x

nx  =  20x

Divide each side by x.

n  =  20

So, the value of n is 20.

Apart from the stuff given above,  if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

WORD PROBLEMS

HCF and LCM  word problems

Word problems on simple equations 

Word problems on linear equations 

Word problems on quadratic equations

Algebra word problems

Word problems on trains

Area and perimeter word problems

Word problems on direct variation and inverse variation 

Word problems on unit price

Word problems on unit rate 

Word problems on comparing rates

Converting customary units word problems 

Converting metric units word problems

Word problems on simple interest

Word problems on compound interest

Word problems on types of angles 

Complementary and supplementary angles word problems

Double facts word problems

Trigonometry word problems

Percentage word problems 

Profit and loss word problems 

Markup and markdown word problems 

Decimal word problems

Word problems on fractions

Word problems on mixed fractions

One step equation word problems

Linear inequalities word problems

Ratio and proportion word problems

Time and work word problems

Word problems on sets and Venn diagrams

Word problems on ages

Pythagorean theorem word problems

Percent of a number word problems

Word problems on constant speed

Word problems on average speed 

Word problems on sum of the angles of a triangle is 180 degree

OTHER TOPICS 

Profit and loss shortcuts

Percentage shortcuts

Times table shortcuts

Time, speed and distance shortcuts

Ratio and proportion shortcuts

Domain and range of rational functions

Domain and range of rational functions with holes

Graphing rational functions

Graphing rational functions with holes

Converting repeating decimals in to fractions

Decimal representation of rational numbers

Finding square root using long division

L.C.M method to solve time and work problems

Translating the word problems in to algebraic expressions

Remainder when 2 power 256 is divided by 17

Remainder when 17 power 23 is divided by 16

Sum of all three digit numbers divisible by 6

Sum of all three digit numbers divisible by 7

Sum of all three digit numbers divisible by 8

Sum of all three digit numbers formed using 1, 3, 4

Sum of all three four digit numbers formed with non zero digits

Sum of all three four digit numbers formed using 0, 1, 2, 3

Sum of all three four digit numbers formed using 1, 2, 5, 6