SURFACE AREA AND VOLUME OF COMBINATION OF SOLIDS QUESTIONS

Question 1 :

A capsule is in the shape of a cylinder with two hemisphere stuck to each of its ends. If the length of the entire capsule is 12 mm and the diameter of the capsule is 3 mm, how much medicine it can hold?

Solution :

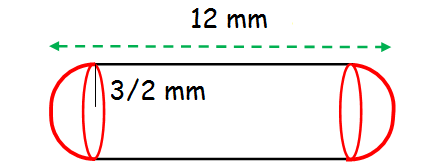
Capacity of capsule 

  =  2 Volume of hemisphere + volume of cylinder 

  =  2(2/3) πr³ + πr²h

  =  (4/3) πr³ + πr²h

Height of Capsule

  =  2 (radius of hemisphere) + height of cylinder

2(3/2) + h  =  12

3 + h =  12

h  =  12 - 3  =  9

=  πr² [(4/3) r + h]

=  (22/7) (3/2)²[(4/3)(3/2) + 9]

 =  (22/7) (9/4)[2 + 9]

 =  (11/7) (9/2)(11)

=  77.78 cm³

Question 2 :

As shown in figure a cubical block of side 7 cm is surmounted by a hemisphere. Find the surface area of the solid.

Solution :

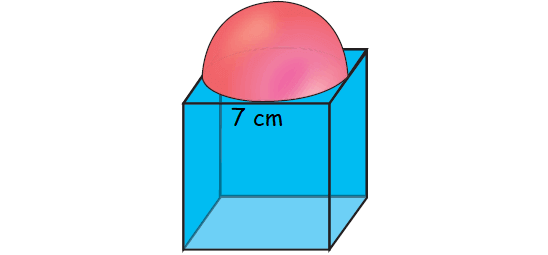
Surface area of solid 

  =  surface area of cube + curved surface area of hemisphere - area of base  of hemisphere 

  = 6a² + 2πr²  - πr² 

  = 6a² + πr²

  =  6(7)² + (22/7) (7/2)² 

  =  294 + 38.5

  =  332.5 cm²

Question 3 :

A right circular cylinder just enclose a sphere of radius r units. Calculate (i) the surface area of the sphere (ii) the curved surface area of the cylinder (iii) the ratio of the areas obtained in (i) and (ii).

Solution :

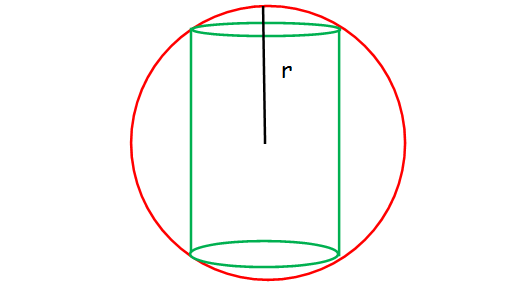
radius of sphere  =  height of cylinder/2

(i) the surface area of the sphere  =  4πr²

(ii) the curved surface area of the cylinder

  =  2π r h

  =  2π r(2r)

  =  4πr²

(iii) the ratio of the areas obtained in (i) and (ii).

  =  4πr²  : 4πr²

  =  1 : 1

Question 4 :

A shuttle cock used for playing badminton has the shape of a frustum of a cone is mounted on a hemisphere. The diameters of the frustum are 5 cm and 2 cm. The height of the entire shuttle cock is 7 cm. Find its external surface area.

Solution :

Surface area of shuttle cock  =  curved surface area of frustum cone + curved surface area of hemisphere

  =  π (R + r) l + 2πr²  ----(1) 

Height of shuttle cock  =  7

radius of hemisphere + height of frustum cone  =  7

1 + h  =  7

h  =  6

l = √(h² + (R - r)²)

l = √(6² + ((5/2) - 1)²)

l = √(36 + (9/4)

l = √153/2

l = 12.36/2

l = 6.18

By applying the value of l in (1), we get 

  =  π ((5/2) + 1) l + 2πr²

  =  π[(7/2)(6.18) + 2 (1)²]

  =  (22/7)[(21.63 + 2]

  =  74.26 cm²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.