SURFACE AREA AND VOLUME OF SPHERES WORKSHEET

Question 1 :

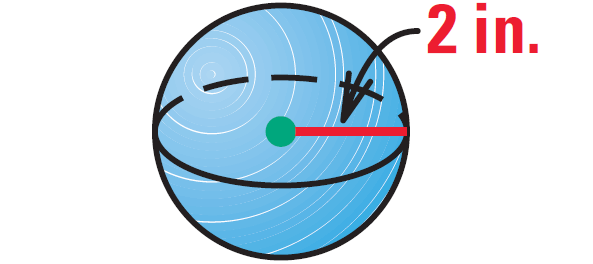
(a) Find the surface area of the sphere shown below. 

(b) When the radius doubles, does the surface area double ?

Question 2 :

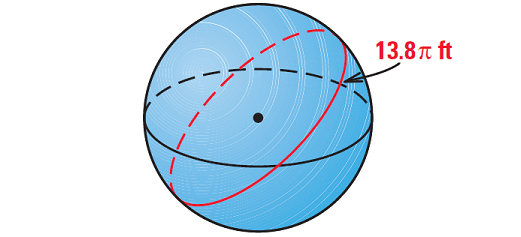
The circumference of a great circle of a sphere is 13.8π feet. What is the surface area of the sphere ? 

Question 3 :

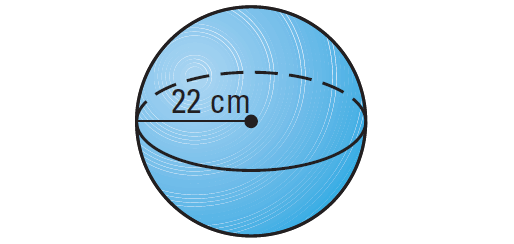
Find the volume of the sphere shown below. 

Question 4 :

A baseball and its leather covering are shown. The baseball has a radius of about 1.45 inches.

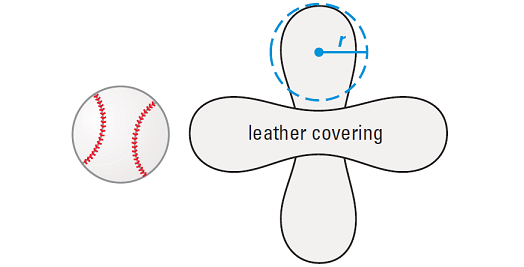
a. Estimate the amount of leather used to cover the baseball. 

b. The surface of a baseball is sewn from two congruent shapes, each of which resembles two joined circles. How does this relate to the formula for the surface area of a sphere ?

Question 5 :

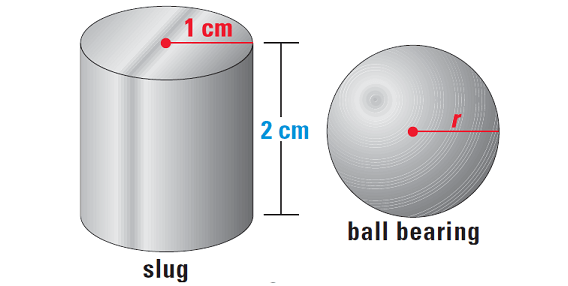
To make a steel ball bearing, a cylindrical slug is heated and pressed into a spherical shape with the same volume. Find the radius of the ball bearing below.

Answers

1. Answer :

Solution (a) : 

Formula for surface area of a sphere : 

S  =  4πr²

Substitute 2 for r. 

S  =  4π (2²)

S  =  4π (4)

S  =  16π

The surface area of the sphere is 16π square inches.

Solution (b) : 

When the radius doubles, 

r  =  2 ⋅ 2

r  =  4 inches

Formula for surface area of a sphere : 

S  =  4πr²

Substitute 4 for r. 

S  =  4π (4²)

S  =  4π (16)

S  =  64π  in²

Because 16π ⋅ 4  =  64π, the surface area of the sphere in part (b) is four times the surface area of the sphere in part (a).

So, when the radius of a sphere doubles, the surface area does not double.

2. Answer :

Draw a sketch.

Begin by finding the radius of the sphere.

Formula for circumference of a circle : 

C  =  2πr

Substitute 13.8π for C.

13.8π  =  2πr

Divide each side by 2π.

6.9  =  r

Formula for surface area of a sphere : 

S  =  4πr²

Substitute 6.9 for r. 

S  =  4π(6.9)²

Simplify.

S  =  4π( 47.61)

Use calculator. 

S  ≈  598  ft²

So, the surface area of the sphere is about 598 square feet.

3. Answer :

Formula for volume of a sphere : 

V  =  4/3 ⋅ πr³

Substitute 22 for r. 

V  =  4/3 ⋅ π(22³)

Simplify.

V  =  4/3 ⋅ π(10648)

V  =  42592/3 ⋅ π

Use calculator.

V  ≈  44602 cm²

The volume of the sphere is about 44602 cubic cm. 

4. Answer :

Solution (a) : 

Because the radius r is about 1.45 inches, the surface area is as follows.

Formula for surface area of a sphere : 

S  =  4πr²

Substitute 1.45 for r. 

S  =  4π(1.45²)

Simplify.

S  =  8.41π

Use calculator. 

S  ≈  26.4  in²

So, the amount of leather used to cover the baseball is about 26.4 square inches.

Solution (b) : 

Because the covering has two pieces, each resembling two joined circles, then the entire covering consists of four circles with radius r.

The area of a circle of radius r is

A  =  πr²

So, the area of the covering can be approximated by

4πr²

This is the same as the formula for the surface area of a sphere.

5. Answer :

To find the radius of the ball bearing, first we need to find the volume of the slug. 

Use the formula for the volume of a cylinder.

V  =  πr²h

Substitute 1 for r and 2 for h. 

V  =  π(1)²(2)

Simplify.

V  =  2π  cm³

To find the radius of the ball bearing, use the formula for the volume of a sphere and solve for r.

Formula for volume of sphere : 

V  =  4/3 ⋅ πr³

Substitute 2π for V. 

2π  =  4/3 ⋅ πr³

Multiply each side by 3. 

6π  =  4πr³

Divide each side by 4π. 

1.5  =  r³

Use a calculator to take the cube root.

1.14  ≈  r

So, the radius of the ball bearing is about 1.14 centimeters.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.