SURFACE AREA AND VOLUME OF SPHERES

Finding the Surface Area of a Sphere

A circle was described as the locus of points in a plane that are a given distance from a point. A sphere is the locus of points in space that are a given distance from a point. The point is called the center of the sphere. A radius of a sphere is a segment from the center to a point on the sphere.

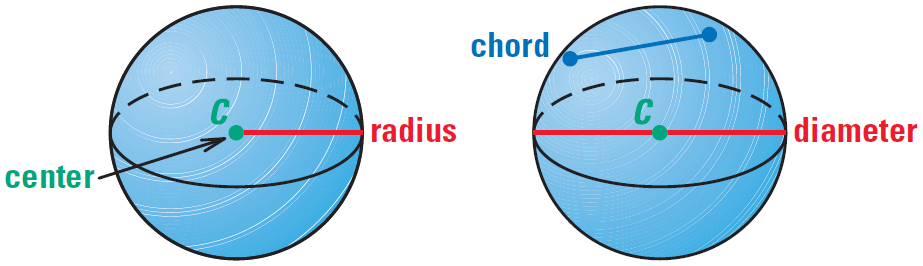
A chord of a sphere is a segment whose endpoints are on the sphere. A diameter is a chord that contains the center. As with circles, the terms radius and diameter also represent distances, and the diameter is twice the radius.

Theorem (Surface Area of a Sphere) :

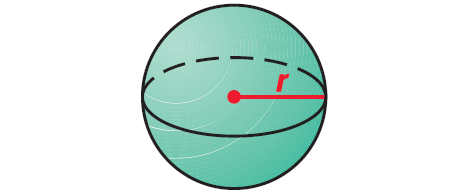
The surface area S of a sphere with radius r is

S = 4πr²

Finding the Volume of a Sphere

Imagine that the interior of a sphere with radius r is approximated by n pyramids, each with a base area of B and a height of r, as shown below. 

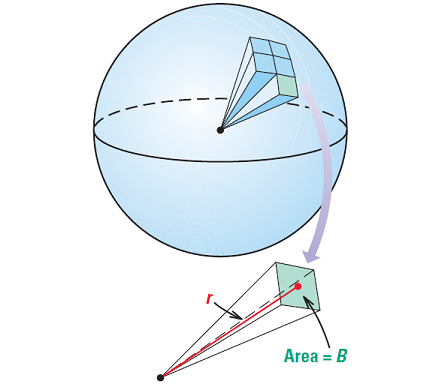
The volume of each pyramid is

=  1/3 ⋅ Br

and the sum of the base areas is

=  nB

The surface area of the sphere is approximately equal to nB, or 4πr². So, we can approximate the volume V of the sphere as follows.

Each pyramid has a volume of 1/3 ⋅ Br

V  ≈  n ⋅ 1/3 ⋅ Br

Regroup factors.

V  =  1/3 ⋅ (nB)r

Substitute 4πr² for nB.

V  ≈  1/3 ⋅ (4πr²)r

Simplify.

V  =  4/3 ⋅ πr³

Theorem (Volume of a Sphere) :

The volume V of a sphere with radius r is

V  =  4/3 ⋅ πr³

Great Circle of a Sphere

If a plane intersects a sphere, the intersection is either a single point or a circle. If the plane contains the center of the sphere, then the intersection is a great circle of the sphere. 

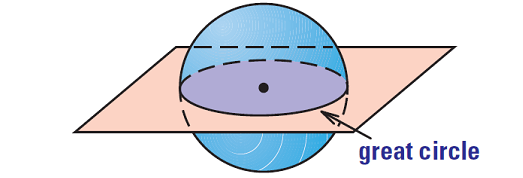
Every great circle of a sphere separates a sphere into two congruent halves called hemispheres. 

Finding the Surface Area of a Sphere

Example 1 :

(a) Find the surface area of the sphere shown below. 

(b) When the radius doubles, does the surface area double ?

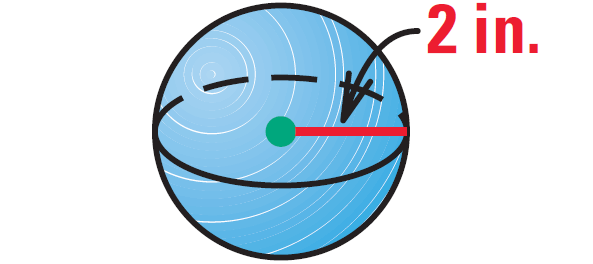
Solution :

Solution (a) :

Formula for surface area of a sphere : 

S  =  4πr²

Substitute 2 for r.

S  =  4π (2²)

S  =  4π (4)

S  =  16π

The surface area of the sphere is 16π square inches.

Solution (b) :

When the radius doubles, 

r  =  2 ⋅ 2

r  =  4 inches

Formula for surface area of a sphere : 

S  =  4πr²

Substitute 4 for r. 

S  =  4π (4²)

S  =  4π (16)

S  =  64π  in²

Because 16π ⋅ 4  =  64π, the surface area of the sphere in part (b) is four times the surface area of the sphere in part (a).

So, when the radius of a sphere doubles, the surface area does not double.

Using a Great Circle 

Example 2 :

The circumference of a great circle of a sphere is 13.8π feet. What is the surface area of the sphere ? 

Solution :

Draw a sketch.

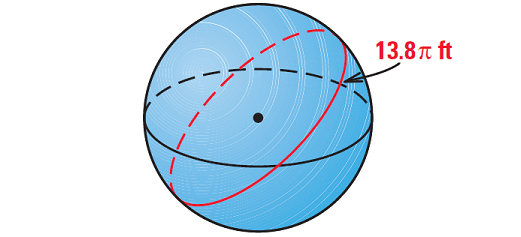
Begin by finding the radius of the sphere.

Formula for circumference of a circle : 

C  =  2πr

Substitute 13.8π for C.

13.8π  =  2πr

Divide each side by 2π.

6.9  =  r

Formula for surface area of a sphere : 

S  =  4πr²

Substitute 6.9 for r. 

S  =  4π(6.9)²

Simplify.

S  =  4π( 47.61)

Use calculator. 

S  ≈  598  ft²

So, the surface area of the sphere is about 598 square feet.

Finding the Volume of a Sphere 

Example 3 :

Find the volume of the sphere shown below. 

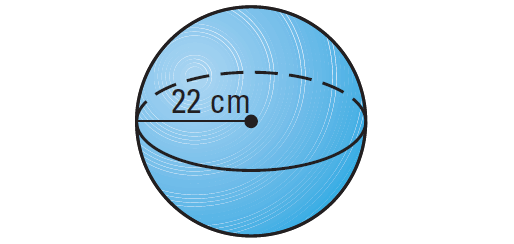
Solution :

Formula for volume of a sphere : 

V  =  4/3 ⋅ πr³

Substitute 22 for r. 

V  =  4/3 ⋅ π(22³)

Simplify.

V  =  4/3 ⋅ π(10648)

V  =  42592/3 ⋅ π

Use calculator.

V  ≈  44602 cm²

The volume of the sphere is about 44602 cubic cm. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.