SURFACE AREA OF CUBE CUBOID AND CYLINDER

Here we are going to see the formulas and example problems to understand the concept of finding surface area of cube, cuboid and cylinder.

Curved surface area

Curved surface area of a solid is the measurement of outer area,where the extension of top and bottom portion wont be included. .

Total surface area

Total surface area of a solid is the measurement of outer area,where the extension of top and bottom portion would be included. 

Now let us see the formulas used to find the surface area of cube, cuboid and cylinder.

Cube 

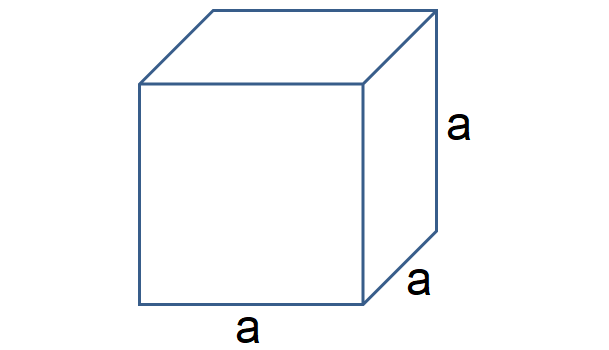
Curved surface area  =  4a

Total surface area  =  6a

Cuboid 

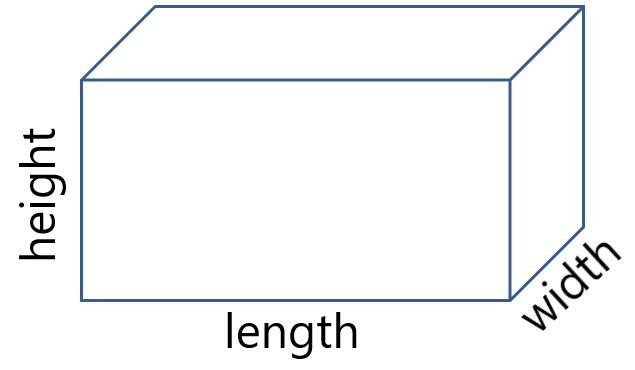
Curved surface area  =  2h(l + w)

Total surface area  =  2 (lw + wh + hl)

Cylinder

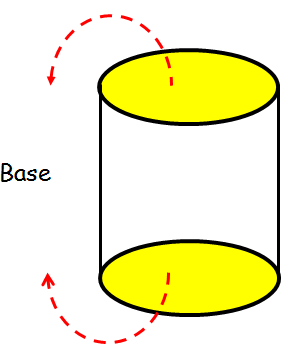
Curved surface area  =  2 π r h

Total surface area  =  2  π r (h + r)

Surface area of cube cuboid and cylinder - Examples

Example 1 :

Daniel is painting the walls and  ceiling of the cuboidal hall with length, width and height of 15 m, 10 m and 7 m respectively. From each can of paint 100 m² of area is painted. How many such cans of paint will he need to paint the room.

Solution :

Since Daniel has to paint the four walls and celing, he has to cover five portions.

Surface area of four walls  =  2h (l + w)

Area of ceiling  =  length ⋅ width

length  =  15 m

width  =  10 m

height  =  7 m

Area has to be painted  =  2h (l + w) + length ⋅ width

  =  2(7) (15 + 10) + 15 ⋅ 10

  =  14 (25) + 150

  =  350 + 150

  =  500 m²

By using 1 can of paint he can cover 100 m²

In order to cover the area of 500 m², he has to buy 5 cans. 

Example 2 :

A company packages its milk powder in cylindrical container whose base has a diameter of 14 cm and height of 20 cm. Company places a label around the surface of the container. If the label is placed 2 cm from top and bottom, what is the area of the label.

Solution :

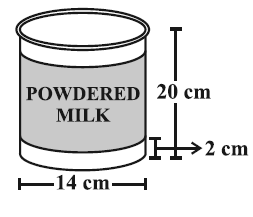
Required area of label placed   =  2Π rh

Height of label  =  20 - 2 - 2  =  16 cm

Radius of cylinder  =  14/2  =  7  cm

Required area  =  2Π rh

  =  2 ⋅ (22/7) ⋅ 16 ⋅ 7

  =  2 ⋅ 22 ⋅ 16

  =  704 cm²

Example 3 :

There are two cuboidal boxes as shown in the adjoining figures. Which box requires the lesser amount of material to make ?

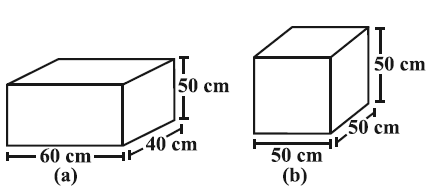
Solution :

In order to find which box requires the lesser amount of material, we have to find the surface area of both figures separately,

Surface are of cuboid  =  2h (l + w)

length of cuboid  =  60 cm

width of cuboid  =  40 cm

height of cuboid  =  50 cm

  =  2 (50) (60 + 40)

  =  100 (100)

  =  10000 cm²

Surface are of cuboid  =  4a

Side length of cube  =  50 cm

  =  4 (50) 

  =  200 cm²

Hence to make the shape cube we need lesser amount of material.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.