SURFACE AREA OF PRISM AND CYLINDER

The surface area of any prism equals the sum of the areas of its faces, which include the floor, roof and walls. Because the floor and the roof of a prism have the same shape, the surface area can always be found as follows.

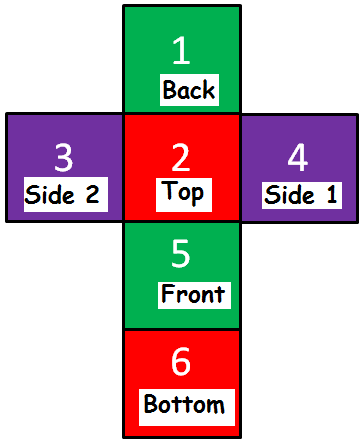
Cube

A cube is a right rectangular prism with square upper and lower bases and a square vertical faces.

Now let us see how to find the surface of square 

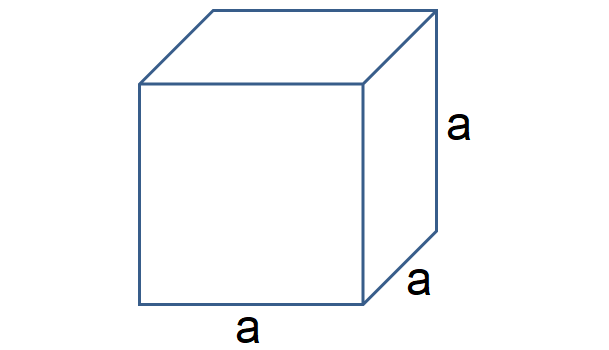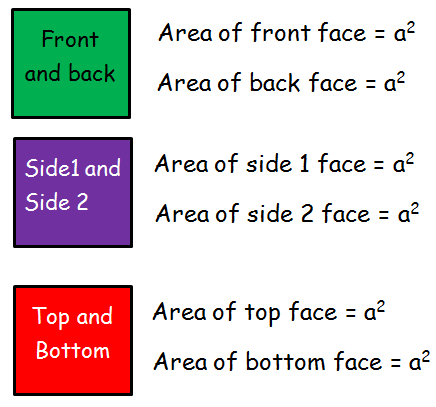
Surface area of cube  =  a² + a² + a² + a² + a² + a² 

=  6a²

Lateral surface area  =  4a²

(Area of side 1, 2, front and back)

Total surface area  =  6a²

(Area of side 1, 2, front, back, top and bottom)

Cuboid

A cuboid is a three-dimensional shape with a length, width, and a height. The cuboid shape has six sides called faces

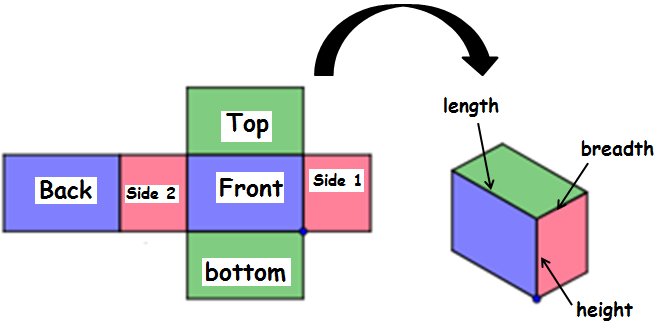
Area of top face  =  (length x breadth) ==> lb

Area of bottom face  =  (length x breadth) ==> lb

Area of front face  =  length x height ==>  lh

Area of back face  =  length x height ==>  lh

Area of side1 face  =  breadth x height ==>  bh

Area of side2 face  =  breadth x height ==>  bh

Surface area of cube  =  lb +  lb + lh + lh + bh + bh

   = 2lb + 2hl + 2bh

   = 2(lb + hl + bh) 

Lateral surface area  =  bh + bh + hl + hl

=  2bh + 2hl  = 2h (l+b)

(Area of side 1, 2, front and back)

Total surface area  =   2(lb + hl + bh) 

(Area of side 1, 2, front, back, top and bottom)

Cylinder

A cylinder is a solid with congruent parallel circular bases connected by a curved surface.

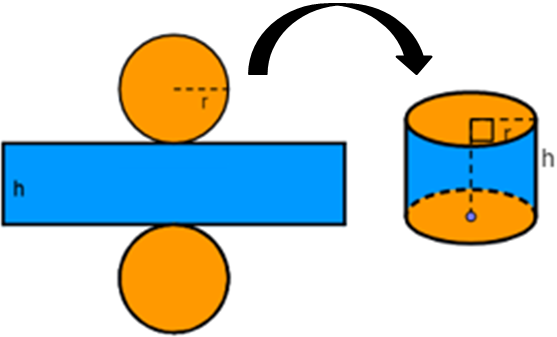
The vertical surface of the cylinder is curved and hence its area is called the curved surface or lateral surface area of the cylinder.

Curved Surface Area of a cylinder is

=  Circumference of the base x Height

=  2πrh square units

Total Surface Area is

=  Area of the Curved Surface + 2 x Base Area

=  2πrh + 2 πr² square units

Sphere

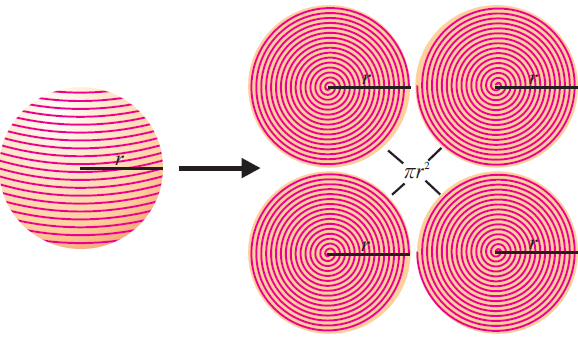
If a circular disc is rotated about one of its diameter, the solid thus generated is called sphere. Thus sphere is a 3- dimensional object which has surface area.

The following activity may help us to visualize the surface area of a sphere as four times the area of the circle with the same radius.

• Take a plastic ball.
• Fix a pin at the top of the ball.
• Wind a uniform thread over the ball so as to cover the whole curved surface area.
• Unwind the thread and measure the length of the thread used.
• Cut the thread into four equal parts.
• Place the strings as shown in the figures.
• Measure the radius of the sphere and the circles formed.

Now, the radius of the sphere is 

=  radius of the four equal circles.

Curved surface area of a sphere is 

=  4πr² square units

Hemisphere

A plane passing through the center of a solid sphere divides the sphere into two equal parts. Each part of the sphere is called a solid hemisphere.

Curved surface area of hemisphere is

=  Curved surface area/2

  =  4πr²/2

=  2πr² square units

Total surface area of hemisphere is

=  curved surface area + area of base 

=  2πr² + πr²

=  3πr² square units

Cone

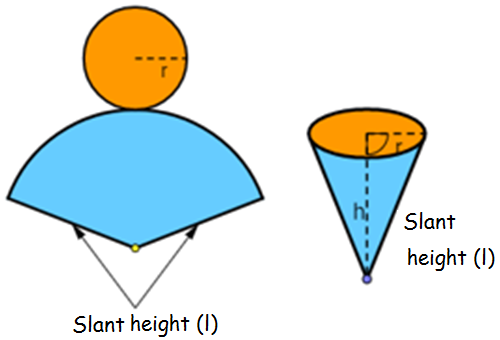
Let us consider a sector with radius l and central angle. Let L denote the length of the arc.

Thus,

2rl/L  =  360°/θ

 L  =  2πl x θ/360° -----(1)

Now, join the radii of the sector to obtain a right circular cone.

Let r be the radius of the cone.

Then,

L  =  2πr

From (1) we obtain,

2πr  =  2πl x (θ/360°)

r  =  l(θ/360°)

(r/l)  =  θ/360°

Let "A" be the area of sector.

Then,

πl²/A  =  360°/θ

So, curved surface area of the cone is 

=  Area of the sector

= πl²(θ°/360°)

=  πl²(r/l)

=  πrl

Total surface area of hemisphere is

=  curved surface area + area of base

=   πrl + πr²

=  πr(l + r)  square units

Triangular Prism

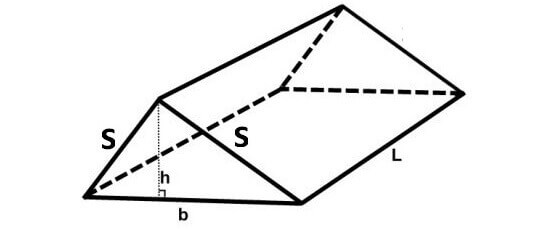
In the above triangular prism, there are five faces. The shape of the base and the two slanting faces is rectangle. The shape of two faces on the left side and right side  is triangle. 

For the given triangular prism, 

Area of the base  =  Lb 

Area of the first slanting face  =  Ls

Area of the other slanting face  =  Ls

Area of the front face  =  (1/2)bh

Area of the back face   =  (1/2)bh

So, surface area is 

=  sum of the area of 5 faces

=  Lb + 2Ls + 2 x (1/2)bh 

=  Lb + 2Ls + bh square units

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.