SURFACE AREA OF PRISMS AND CYLINDERS WORKSHEET

Problem 1 :

Find the surface area of a right rectangular prism with a height of 8 inches, a length of 3 inches, and a width of 5 inches.

Problem 2 :

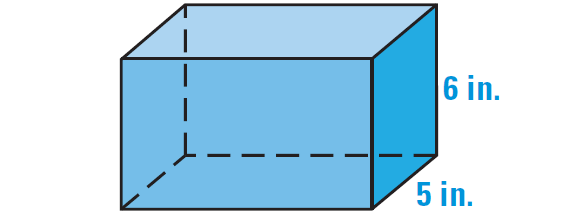
Find the surface area of the right prism shown below.

Problem 3 :

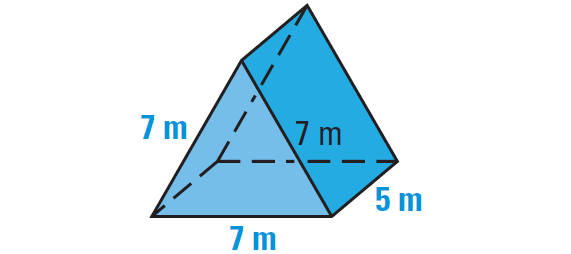
Find the surface area of the right prism shown below.

Problem 4 :

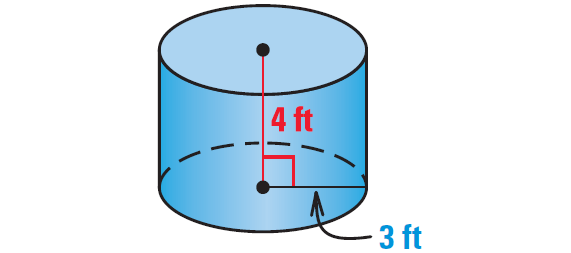
Find the surface area of the right cylinder shown below. 

Problem 5 :

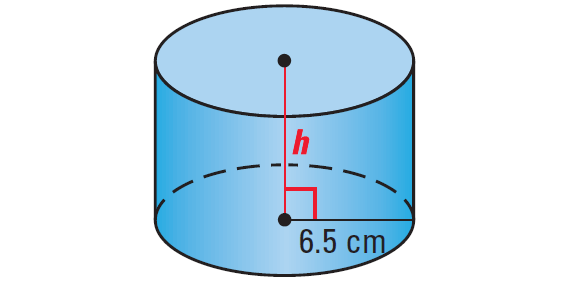
Find the height of a cylinder which has a radius of 6.5 centimeters and a surface area of 592.19 square centimeters.

Answers

Problem 1 :

Find the surface area of a right rectangular prism with a height of 8 inches, a length of 3 inches, and a width of 5 inches.

Answer :

Draw a sketch. 

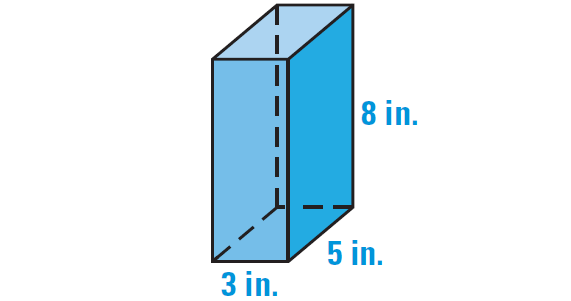
The prism has 6 faces, two of each of the following :

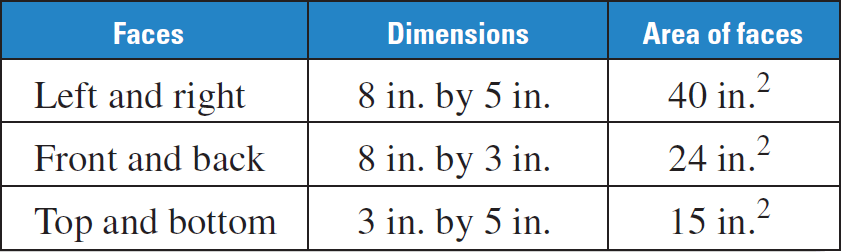
The surface area of the prism is 

S  =  2(40) + 2(24) + 2(15)

S  =  80 + 48 + 30

S  =  158

So, the surface area of the right rectangular prism is 158 square inches.

Problem 2 :

Find the surface area of the right prism shown below.

Answer :

Each base measures 5 inches by 10 inches with an area of

B  =  5(10)

B  =  50 in²

The perimeter of the base is

P = 30 in.

and the height is

h = 6 in.

The surface area is 

S  =  2B + Ph

S  =  2(50) + 30(6)

S  =  100 + 180

S  =  280

So, the surface area of the right prism is 280 square inches.

Problem 3 :

Find the surface area of the right prism shown below.

Answer :

In the above prism, each base is an equilateral triangle with a side length s, of 7 meters as shown below.

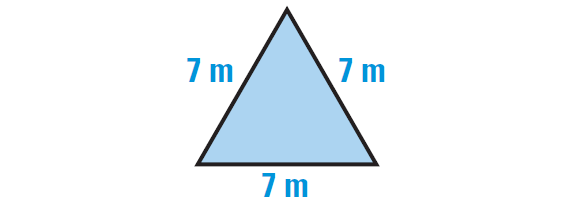
Using the formula for the area of an equilateral triangle, the area of each base is

B  =  1/4 ⋅ √3(s²)

B  =  1/4 ⋅ √3(7²)

B  =  1/4 ⋅ 49√3

B  =  49√3 / 4  m²

The perimeter of each base is

P  =  21 m

and the height is

h  =  5 m

The surface area is 

S  =  2B + Ph

S  =  2(49√3/4) + 21(5)

S  =  49√3/2 + 105

Use calculator.

S  ≈  147  m²

So, the surface area of the right prism is about 147 square meters.

Problem 4 :

Find the surface area of the right cylinder shown below. 

Answer :

Each base has a radius of 3 feet, and the cylinder has a height of 4 feet.

Formula for surface area of a cylinder : 

S  =  2πr² + 2πrh

Substitute. 

S  =  2π(3)² + 2π(3)(4)

S  =  18π + 24π

S  =  42π

Use calculator. 

S ≈  131.95

So, the surface area of the right cylinder is about 132 square meters.

Problem 5 :

Find the height of a cylinder which has a radius of 6.5 centimeters and a surface area of 592.19 square centimeters.

Answer :

Draw a sketch.

Formula for surface area of a cylinder : 

S  =  2πr² + 2πrh

Substitute. 

592.19  =  2π(6.5)² + 2π(6.5)(4)

592.19  =  84.5π + 13πh

Subtract 84.5π from each side. 

592.19 - 84.5π  =  13πh

Simplify.

 326.73  ≈  13πh

Divide each side by 13π.

 326.73/13π  ≈  h

Use calculator and simplify.

 8  ≈  h

So, the height of the cylinder is about 8 cm. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.