SURFACE AREA OF PYRAMID WITH RECTANGULAR BASE

Pyramid is basically a 3D shape. Even though we have formulas to find surface area of pyramid with rectangular base, the basic idea of finding surface is to add the areas of all the faces.  

To understand how to find surface area of a pyramid with rectangular base, let us consider the pyramid given below. 

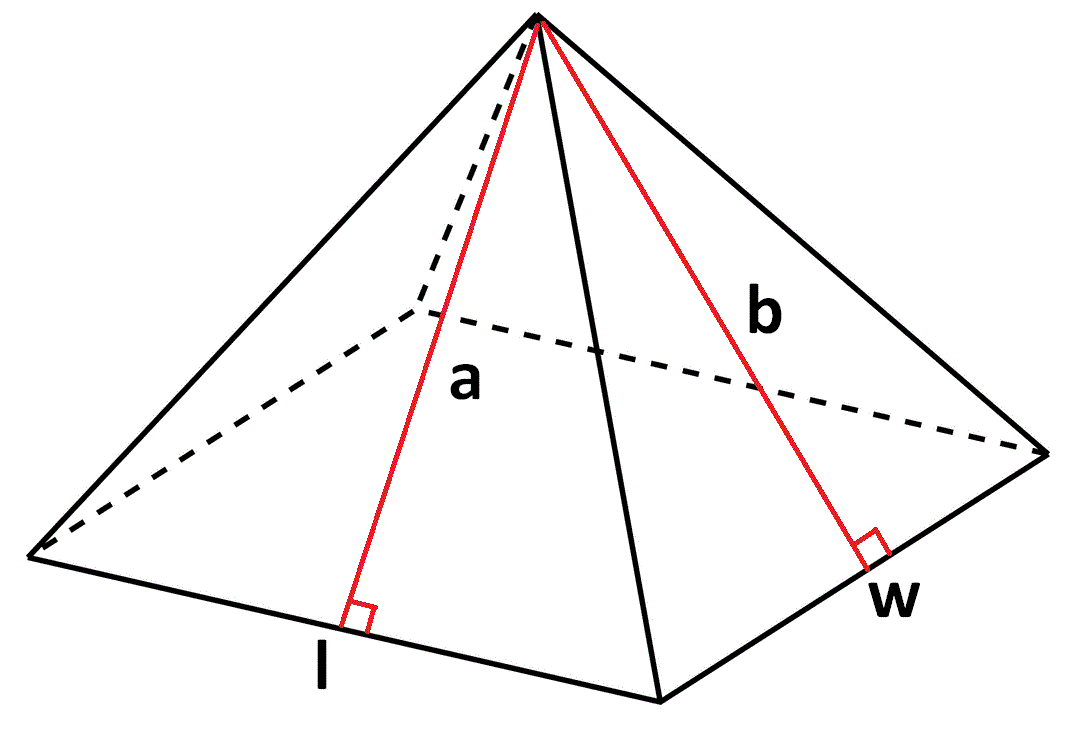
Here is the basic idea to find surface area of the above pyramid. 

Surface Area  =  Sum of areas of all five faces (Including the base)

For any pyramid, if the shape of the base is rectangle, then we will have four side walls.

The shape of each side wall will be a triangle.

In the above pyramid, the base is a rectangle with length "l" and width "w". 

Two opposite triangles (being as side walls) with base "l" and height "a" will have equal area.

The other two opposite triangles (being as side walls) with base "w" and height "b" will have equal area.

Let us find the area of each face separately. 

Area of the base is

=  l x w  =  lw

Area of two side walls (Triangles having base "l" and height "a") is 

=  2 x (1/2) x l x a  

=  la

Area of other two side walls (Triangles having base "w" and height "b")

=  2 x (1/2) x w x b

=  wb

Surface area of the above pyramid is 

=  lw + la + wb

This is the formula to find surface area of a pyramid with rectangle base. 

Practice Problems

Problem 1 : 

Find the surface area of the pyramid shown below.

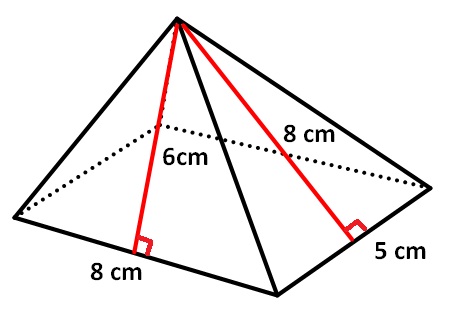
Solution : 

Surface area of the pyramid is

=  Sum of areas of all 5 faces

In the above pyramid, the base is a rectangle with length 8 cm and width 5 cm.

Let us find the area of each face separately. 

Area of the base is

=  8 x 5

=  40 sq.cm

Area of two side walls (Triangles having base 8 cm and height 6 cm) is

=  2 x (1/2) x 8 x 6

=  48 sq. cm

Area of other two side walls (Triangles having base 5 cm and height 8 cm) is

=  2 x (1/2) x 5 x 8

=  40 sq. cm

Surface area of the above pyramid is

=  40 + 48 + 40

=  128 sq.cm

Problem 2 : 

Find the surface area of the pyramid shown below.

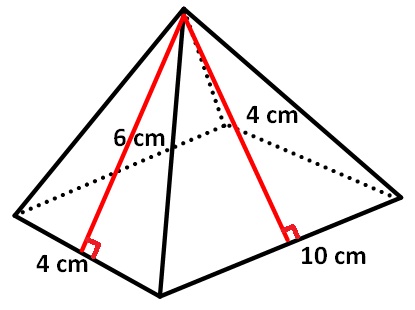
Solution : 

Surface area of the pyramid is

=  Sum of areas of all 5 faces

In the above pyramid, the base is a rectangle with length 10 cm and width 4 cm. 

Let us find the area of each face separately. 

Area of the base is

=  10 x 4

=  40 sq.cm

Area of two side walls (Triangles having base 10 cm and height 4 cm) is 

=  2 x (1/2) x 10 x 4

=  40 sq. cm

Area of other two side walls (Triangles having base 4 cm and height 6 cm )

=  2 x (1/2) x 4 x 6

=  24 sq. cm

 Surface area of the above pyramid is

=  40 + 40 + 24

=  104 sq.cm

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.