SURFACE AREA OF PYRAMID

Pyramid is basically a 3D shape. Even though we have different formulas to find surface area of different kinds of pyramids, the basic idea of finding surface area of a pyramid is to add the areas of all the faces.  

To understand how to find surface area of a pyramid, let us consider the pyramid with square base.

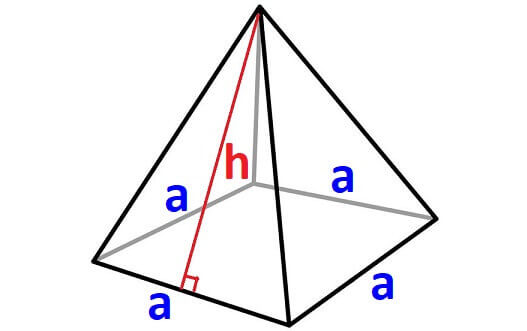
Here is the basic idea to find surface area of the above pyramid. 

Surface Area  =  Sum of areas of all five faces (Including the base)

For any pyramid, if the shape of the base is square, then we will have four side walls. The shape of each side wall will be a triangle with equal area.  

In the above pyramid, the base is a square with side length "a" and each wall is a triangle with base "a" and height "h"

Let us find the area of each face separately. 

Area of the base  =  a x a  =  a²

Area of each side wall  =  (1/2)ah 

Area of all four side walls  =  4 x (1/2)ah  =  2ah 

Surface area of the above pyramid is

  =  a² + 2ah

This is the formula to find surface area of a pyramid with square base. 

We can apply the above explained basic idea to find surface area of a pyramid with triangular base. 

Let us find surface area of a pyramid with triangular base. 

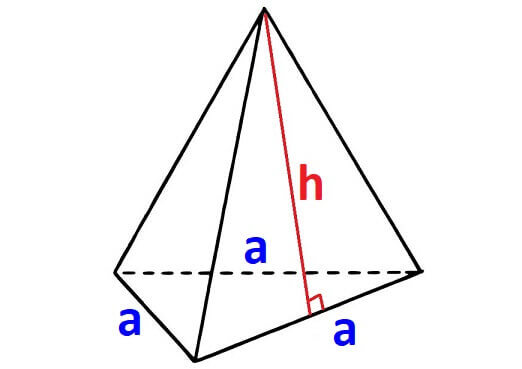
For any pyramid, if the shape of the base is equilateral  triangle, then we will have three side walls. The shape of each side wall will be a triangle with equal area.  

In the above pyramid, the base is an equilateral triangle with side length "a". 

And each wall is a triangle with base "a" and height "h"

Let us find the area of each face separately. 

Area of the base  =  (√3/4)a²

Area of each side wall  =  (1/2)ah 

Area of all 3 side walls  =  3 x (1/2)ah  =  (3/2)ah 

Surface area of the above pyramid is

=  (√3/4)a² + (3/2)ah

This is the formula to find surface area of a pyramid with equilateral triangle base. 

Note :

If the base is not equilateral triangle and it is either scalene triangle or isosceles triangle, then the area of side walls will not be equal. We have to find area of each side wall separately.  

Practice problems

Problem 1 : 

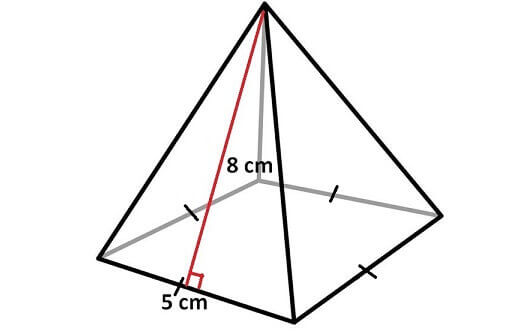
Find the surface area of the pyramid shown below.

Solution : 

Surface area of the pyramid is

=  Sum of areas of all 5 faces

In the above pyramid, the base is a square with side length 5 cm and each wall is a triangle with base 5 cm and height 8 cm.

Let us find the area of each face separately. 

Area of the base  =  5 x 5  =  25 sq.cm

Area of each side wall  =  (1/2) x 5 x 8  =  20 sq.cm 

Area of all 4 side walls  =  4 x 20  =  80 sq.cm 

Surface area of the above pyramid is

=  25 + 80

=  105 sq.cm

Problem 2 : 

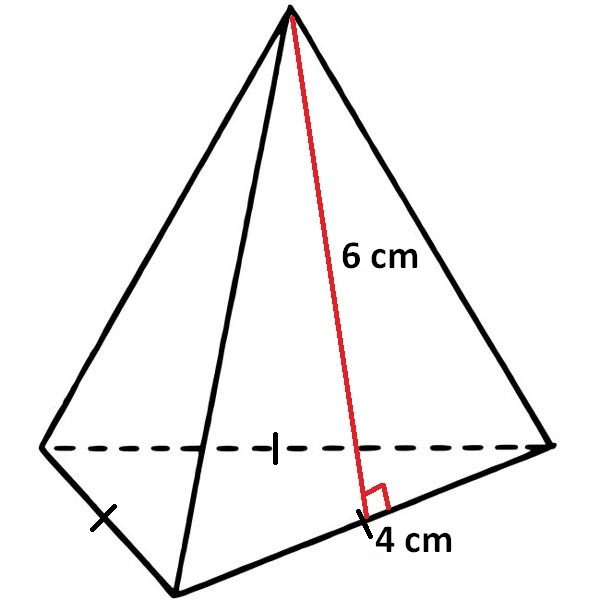
Find the surface area of the pyramid shown below.

Solution : 

Surface area of the pyramid is

=  Sum of areas of all 4 faces

In the above pyramid, the base is an equilateral triangle with side length 4 cm and each wall is a triangle with base 4 cm and height 6 cm.

Let us find the area of each face separately. 

Area of the base  =  (√3/4) x 4²  =  4√3 sq.cm

Area of each side wall  =  (1/2) x 4 x 6  =  12 sq.cm 

Area of all 3 side walls  =  3 x 12  =  36 sq.cm 

Surface area of the above pyramid is 

=  4√3 + 36

=  4(√3 + 9)  sq. cm

Problem 3 :

Find the surface area of the pyramid shown below.

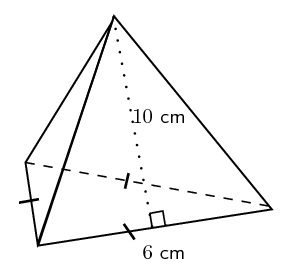
Solution : 

Surface area of the pyramid is

=  Sum of areas of all 4 faces

In the above pyramid, the base is an equilateral triangle with side length 6 cm and each wall is a triangle with base 6 cm and height 10 cm.

Let us find the area of each face separately. 

Area of the base  =  (√3/4) x 6²  =  9√3 sq.cm

Area of each side wall  =  (1/2) x 6 x 10  =  30 sq.cm 

Area of all 3 side walls  =  3 x 30  =  90 sq.cm 

Surface area of the above pyramid is

=  (9√3 + 90)

=  9(√3 + 10)  sq.cm

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.