SYMMETRIC RELATION

Let R be a relation defined on the set A.

If R is symmetric relation, then

R  =  {(a, b), (b, a) / for all a, b ∈ A}

That is, if "a" is related to "b", then "b" has to be related to "a" for all "a" and "b" belonging to A. 

In simple terms, 

a R b -----> b R a

Example :

Let A be the set of two male children in a family and R be a relation defined on set A as

R  =  "is brother of".

Verify whether R is symmetric. 

Solution :

Let a, b ∈ A.  

If "a" is brother of "b", then "b" has to be brother of "a". 

Clearly,

R  =  {(a, b), (b, a)}

So, R is symmetric. 

Solved Problems

Problem 1 :

Let A  =  {1, 2, 3} and R be a relation defined on set A as

R  = {(1, 1), (2, 2), (3, 3), (1, 2)}

Verify R is symmetric. 

Solution :

To verify whether R is symmetric, we have to check the condition given below for each ordered pair in R.

That is, 

(a, b) -----> (b, a)

Let's check the above condition for each ordered pair in R. 

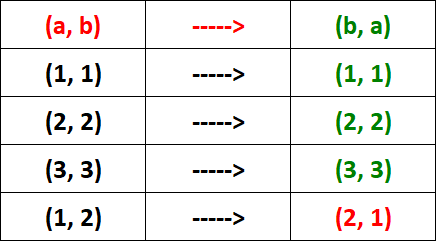
From the table above, if R is symmetric, for the ordered pair (1, 2), we must have (2, 1) in R. 

But, we don't have (2, 1) in R. 

So, R is not symmetric. 

Problem 2 :

Let A  =  {1, 2, 3} and R be a relation defined on set A as

R  = {(1, 1), (2, 2), (1, 2), (2, 1)}

Verify R is symmetric. 

Solution :

To verify whether R is transitive, we have to check the condition given below for each ordered pair in R.

That is, 

(a, b) -----> (b, a)

Let's check the above condition for each ordered pair in R. 

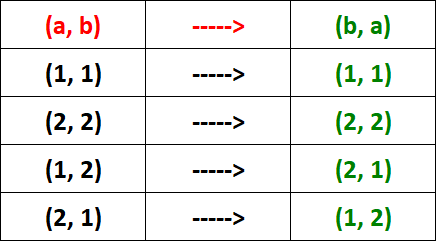
From the table above, it is clear that R is symmetric.

Problem 3 :

Let A  =  {1, 2, 3} and R be a relation defined on set A as

R  = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 1), (2, 3), (3, 2)}

Verify R is symmetric. 

Solution :

To verify whether R is transitive, we have to check the condition given below for each ordered pair in R.

That is, 

(a, b) -----> (b, a)

Let's check the above condition for each ordered pair in R.

From the table above, it is clear that R is symmetric.

Related Topics

Reflexive relation

Transitive relation

Equivalence relation

Identity relation

Inverse relation

Difference between reflexive and identity relation

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.