SYMMETRY

Symmetry is an important geometrical concept commonly seen in nature and is used in every field of our life. Artists, manufacturers, designers, architects and others make use of the idea of symmetry. The beehives, flowers, tree leaves, hand kerchief, utensils have symmetrical design.

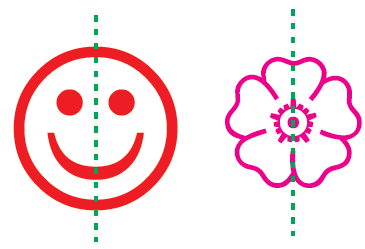
It refers to the exact match in shape and size between two halves of an object. If we fold a picture in half and both the halves-left half and right half - match exactly then we say that the picture is symmetrical

A butterfly is also an example of a symmetrical form. If a line is drawn down the centre of the butterfly’s body, each half of the butterfly looks the same.

y is of different types. Here we discuss about

1. Line of symmet-ry or axis of symmetry

2. Mirror symmetry

3. Rotational symmet-ry

1. Line of symmet-ry

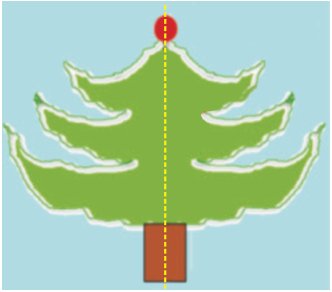
In the figure given below the dotted lines divide the figure into two identical parts. If figure is folded along the line, one half of the figure will coincide exactly with the other half. This dotted line is known as line of symmet-ry. 

When a line divides a given figure into two equal halves such that the left and right halves matches exactly then we say that the figure is symmetrical about the line. This line is called the line of symmet-ry.

Activity 1 :

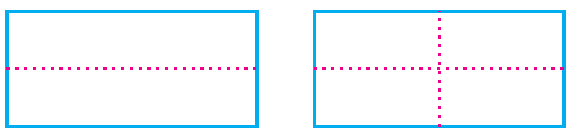
Take a rectangular sheet of paper. Fold it once lengthwise, so that one half fits exactly over the other half and crease the edges. Now open it, and again fold it once along its width.

Activity 2 :

One of the two set squares in your geometry box has angle of measure 30°, 60°, 90°.Take two such identical set squares. Place them side by side to form a ‘kite’ as shown in the figure.

How many lines of symmet-ry does the shape have?

You observe that this kite shape figure has one line of symmetry about its vertical diagonal

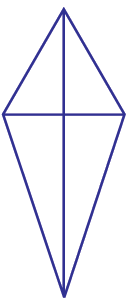
Activity 3 :

For the given regular polygons find the lines of symmet-ry by using paper folding method and also draw the lines of symmetry by dotted lines.

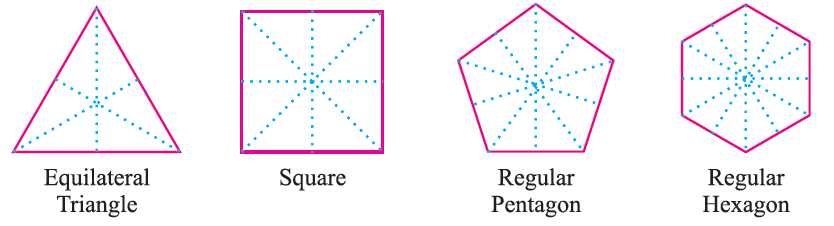
In the above paper foldings, you observe that

(i) An equilateral triangle has three lines of symmet-ry.

(ii) A square has four lines of symmet-ry

(iii) A regular pentagon has five lines of symmet-ry.

(iv) A regular hexagon has six lines of symmet-ry.

Each regular polygon has as many lines of symmet-ry as it has sides.

Some objects and figures have no line of symmet-ry.

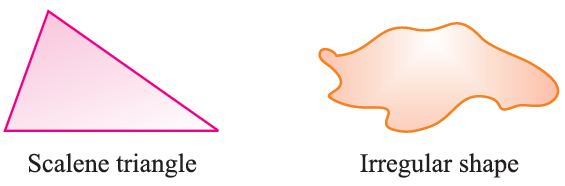
The above figures have no line of symmet-ry; because these figures are not symmetrical. We can say that these figures are asymmetrical.

2. Mirror line symmet-ry

When we look into a mirror we see our image is behind the mirror. This image is due to reflection in the mirror. We know that the image is formed as far behind the mirror as the object is in front of it.

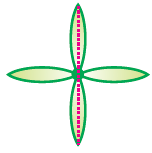
In the above figure if a mirror is placed along the line at the middle, the half part of the figure reflects through the mirror creating the remaining identical half. In other words, the line where the mirror is placed divides the figure into two identical parts in given figure. They are of the same size and one side of the line will have its reflection exactly at the same distance on the other side. Thus it is also known as mirror line symmet-ry.

While dealing with mirror reflection, we notice that the left-right changes as seen in the figure

3 Rotational Symmet-ry

Look at the following figures showing the shapes that we get, when we rotate about its centre ‘O’ by an angle of 90 degree  or 180 degree

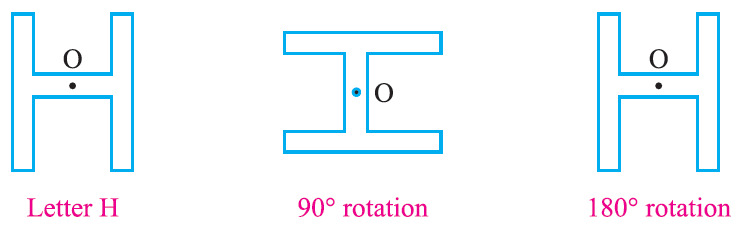
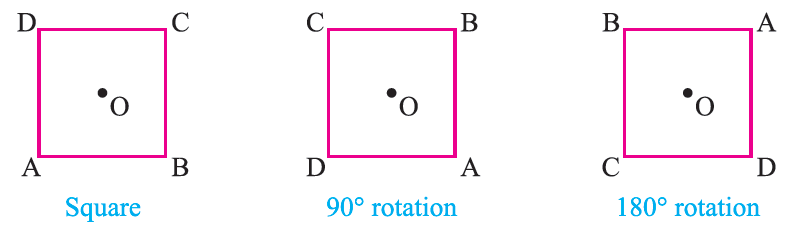
In the case of a square, we get exactly the same shape after it is rotated by 90 degree while in the case of a rectangle, we get exactly the same shape after it is rotated by 180° such figures which can be rotated through an angle less than 360° to get the same shape are said to have rotational symmet-ry.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.