SYSTEM OF LINEAR EQUATIONS WITH UNIQUE SOLUTION
Consider the following system of linear equations given in slope-intercept form.
y = m1x + b1
(slope = m1 and y-intercept = b1)
y = m2x + b2
(slope = m2 and y-intercept = b2)
If the above system of linear equations has unique solution or only one solution, then it has to satisfy the following condition.
m1 ≠ m2
We already know that the graph of any linear equation will be a line.
If two lines have different slopes (m1 ≠ m2), then the lines intersect in only one point and the system has unique solution or only one solution.
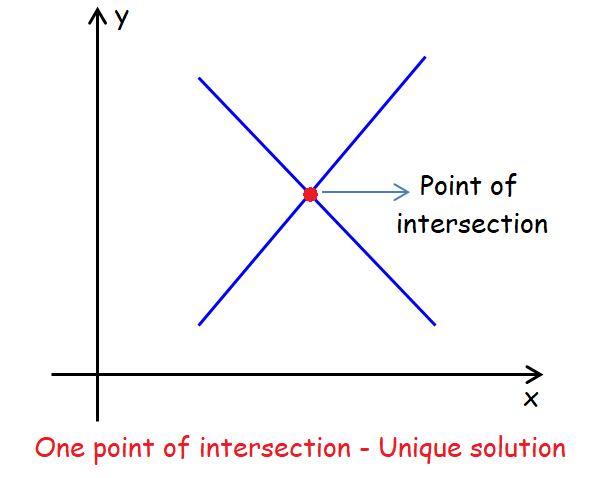
In a system of equations with two variables, let the slopes be not equal (m1 ≠ m2).
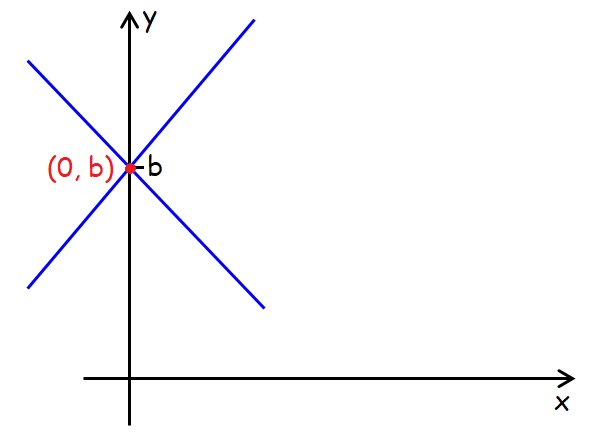
What if there is same y-intercept, say 'b'?
In a system of two linear equations, if the slopes are not equal (m1 ≠ m2), then the system has unique solution or only one solution. It does not matter whether there is same y-intercept or different y-intercepts.
If there is same y-intercept, say 'b', the unique solution is
(0, b)
Note :
If the system of linear equations is given in general form or standard form, write them in slope-intercept form and proceed as explained above.
General Form :
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
Standard Form :
a1x + b1y = c1
a2x + b2y = c2
Examples 1-5 : Determine whether the following systems of linear equations have unique solution.
Example 1 :
y = 2x + 5
y = 3x - 2
Solution :
y = 2x + 5 ----> slope m = 2
y = 3x - 2 ----> slope m = 3
In the above two linear equations, the slopes are different.
So, the lines intersect in only one point.
Hence, the system has unique solution.
Example 2 :
y = -2x + 5
y = -2x + 3
Solution :
y = -2x + 5 ----> slope m = -2
y = -2x + 1 ----> slope m = -2
In the above two linear equations, slopes are equal.
Hence, the system has no unique solution.
Example 3 :
y = 3x - 2
3y = 6x
Solution :
y = 3x - 2 ----> slope m = 3
The second equation 3y = 6x is not in slope intercept form. Divide both sides by 3 to get the equation in slope- intercept form.
y = 2x
y = 2x ----> slope m = 2
In the given two linear equations, the slopes are different.
So, the lines intersect in only one point.
Hence, the system has unique solution.
Example 4 :
3x + y - 1 = 0
2x + y + 5 = 0
Solution :
The equations are not in slope-intercept form.
Write them in slope-intercept form.
|
3x + y - 1 = 0 y = -3x + 1 |
2x + y + 5 = 0 y = -2x - 5 |
y = -3x + 1 ----> slope m = -3
y = -2x - 5 ----> slope m = -2
In the given two linear equations, the slopes are different.
So, the lines intersect in only one point.
Hence, the system has unique solution.
Example 5 :
2x - y = 1
4x + y = 5
Solution :
The equations are not in slope-intercept form.
Write them in slope-intercept form.
|
2x - y = 1 -y = -2x + 1 y = 2x - 1 |
4x + y = 5 y = -4x + 5 |
In the given two linear equations, the slope are different.
So, the lines intersect in only one point.
Hence, the system has unique solution.
Example 6 :
Determine whether the following system of equations has unique solution. If so, find the solution.
y = 3x - 1
y = 2x - 5
Solution :
y = 3x - 1 ----> slope m = 3
y = 2x - 5 ----> slope m = 2
In the given two linear equations, the slopes are different.
So, the lines intersect in only one point.
Hence, the system has unique solution.
Solving for x and y :
y = 3x - 1 ----(1)
y = 2x - 5 ----(2)
Substitute '3x - 1' for y in (2).
3x - 1 = 2x - 5
x = -4
Substitute x = -4 in (1).
y = 3(-4) - 1
y = -12 - 1
y = -13
Therefore, the solution is
x = -4 and y = -13
Example 7 :
Determine whether the following system of equations has unique solution. If so, find the solution.
y = -2x + 9
y = 5x + 9
Solution :
y = -2x + 9 ----> slope m = -2
y = 5x + 9 ----> slope m = 5
In the given two linear equations, the slopes are different.
So, the lines intersect in only one point.
Hence, the system has unique solution.
There is same y-intercept '9' in both the equations.
So, the point of intersection of the two lines is y-intercept, that is (0, 9)
Therefore, the solution is
x = 0 and y = 9
Example 8 :
In the following system of linear equations, k is a constant and x and y are variables. For what value of k will the system of equations have unique solution?
kx - y = 4
10x - 5y = 7
Solution :
The equations are not in slope-intercept form.
Write them in slope-intercept form.
|
kx - y = 4 -y = -kx + 4 y = kx - 4 |
10x - 5y = 7 -5y = -10x + 7 5y = 10x - 7 y = 2x - 7/5 |
y = kx - 4/3 ----> slope m = k
y = 2x - 7/5 ----> slope m = 2
If the system has unique solution, then the slopes must not be equal.
k ≠ 2
When k ≠ 2, the system has unique solution.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
10 Hard SAT Math Questions (Part - 34)
Nov 15, 25 08:00 AM
10 Hard SAT Math Questions (Part - 34) -
Algebra Word Problems Worksheet with Answers
Nov 10, 25 06:30 PM
Algebra Word Problems Worksheet with Answers -
Tricky SAT Math Problems Solved Easily
Nov 09, 25 07:02 PM
Tricky SAT Math Problems Solved Easily


