SYSTEMS OF LINEAR INEQUALITIES

A system of linear inequalities is a set of two or more linear inequalities containing two or more variables.

The solutions of a system of linear inequalities are all of the ordered pairs that satisfy all the linear inequalities in the system.

Identifying Solutions of Systems of Linear Inequalities

Example 1 : 

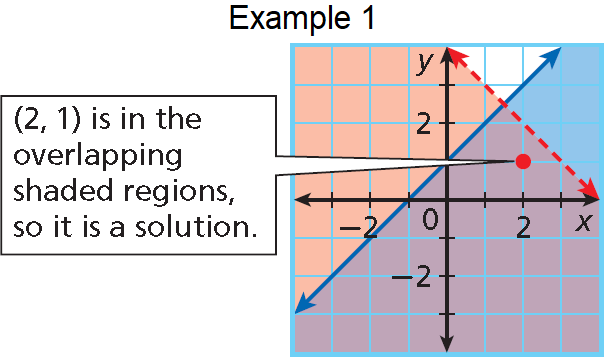
Tell whether the ordered pair (2, 1) is a solution of the following system.

y < -x + 4

y ≤ x + 1

Solution : 

(2, 1) is a solution to the system, because it satisfies both inequalities.

Example 2 : 

Tell whether the ordered pair (2, 0) is a solution of the following system.

y ≥ 2x

y < x + 1

Solution :

(2, 0) is not a solution to the system, because it does not satisfy both inequalities.

Solving a System of Linear Inequalities by Graphing

To show all the solutions of a system of linear inequalities, graph the solutions of each inequality. The solutions of the system are represented by the overlapping shaded regions.

Below are the graphs of example 1 and example 2 explained above.

Example 3 : 

Graph the following system of linear inequalities. Give two ordered pairs that are solutions and two that are not solutions.

8x + 4y ≤ 12

y > (1/2)x - 2

Solution : 

Solve the first inequality for y.

8x + 4y ≤ 12

4y ≤ 12 - 8x

y ≤ 3 - 2x

Graph the system.

y ≤ 3 - 2x

y > (1/2)x - 2

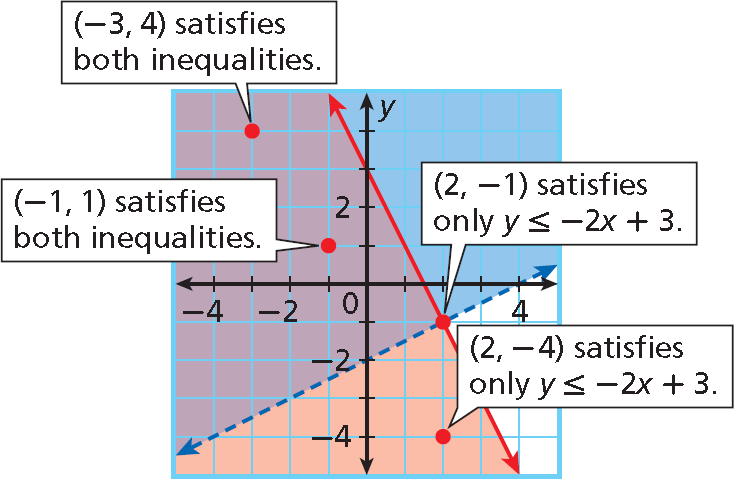
(-1, 1) and (-3, 4) are solutions.

(2, -1) and (2, -4) are not solutions.

Graphing Systems with Parallel Boundary Lines

Graph each system of linear inequalities. Describe the solutions.

Example 4 : 

y < 2 x - 3

y > 2x + 2

Solution : 

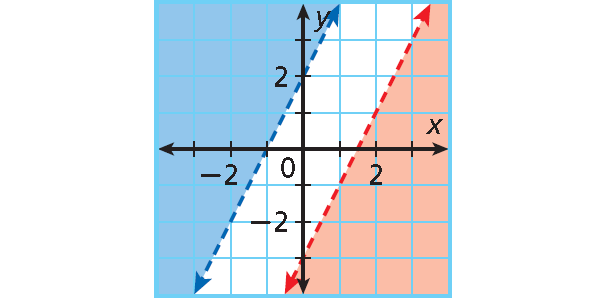
This system has no solution.

Example 5 : 

y > x - 3

y ≤ x + 1

Solution :

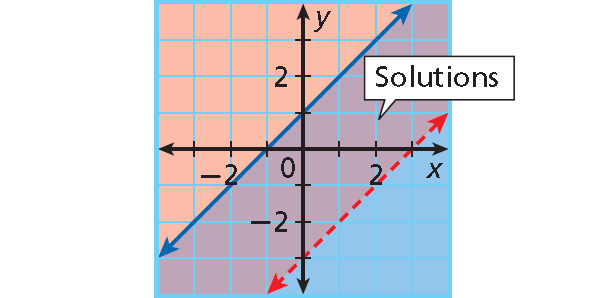
The solutions are all points between the parallel lines and on the solid line.

Example 6 : 

y ≤ - 3x - 2

y ≤ -3x + 4

Solution :

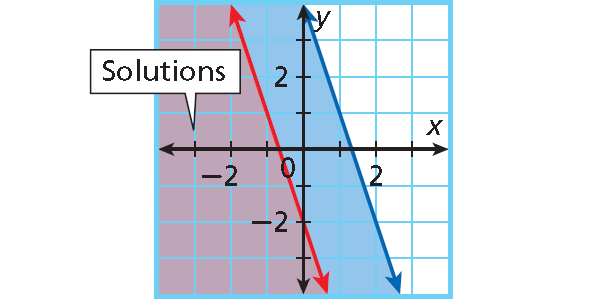
The solutions are the same as the solutions of y ≤ -3x - 2.

Business Application

Example 7 : 

A surf shop makes the profits given in the table. The shop owner sells at least 10 surfboards and at least 20 wakeboards per month. He wants to earn at least $2000 a month. Show and describe all possible combinations of surfboards and wakeboards that the store owner needs to sell to meet his goals. List two possible combinations.

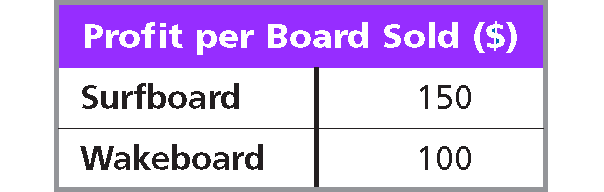
Solution : 

Step 1 : 

Write a system of inequalities. Let x represent the number of surfboards and y represent the number of wakeboards.

x ≥ 10 ---> He sells at least 10 surfboards.

y ≥ 20 ---> He sells at least 20 wakeboards.

He wants to earn a total of at least $2000.

150x + 100y ≥ 2000

Step 2 : 

Graph the system.

The graph should be in only the first quadrant because sales are not negative.

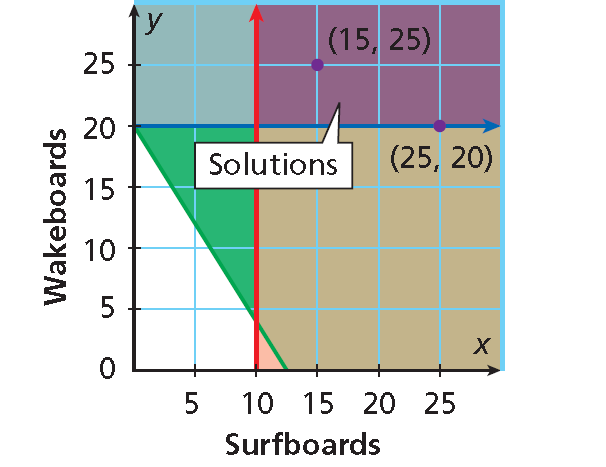
Step 3 : 

Describe all possible combinations. To meet the sales goals, the shop could sell any combination represented by an ordered pair of whole numbers in the solution region. Answers must be whole numbers because the shop cannot sell part of a surfboard or wakeboard. 

Step 4 : 

List two possible combinations.

Two possible combinations are :

15 surfboards and 25 wakeboards

25 surfboards and 20 wakeboards

Example 8 :

The girls’ swim team is hosting a fund raiser. They would like to raise at least $500. They are selling candles for $5 and flower arrangements for $6. The girls estimate that at most they will sell 200 items.

• Write a system of inequalities to represent this situation

• Graph each inequality on the grid.

• 120 candles have been sold. Use your graph to determine a reasonable number of flower arrangements that must be sold in order for the girls to reach their goal of at least $500. Justify your answer.

Solution :

Let x be the number of candles and number of flower arrangements be y.

x + y ≥ 500

5x + 6y ≤ 200

Finding x and y-intercepts :

Put x = 0, y = 500

Put y = 0, x = 500

From 5x + 6y ≤ 200

Put x = 0, y = 200/6 ==> 33.3

Put y = 0, x = 200/5 ==> 40

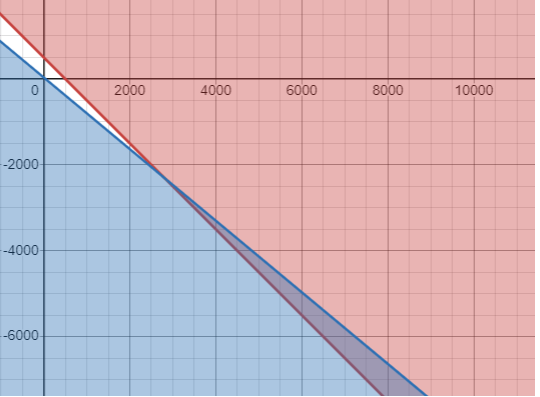
When x = 120

y = 200 - 120

y = 80

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.