TANGENT LINES TO CIRCLES WORKSHEET
Problem 1 :
Determine if the line segment AB is tangent to circle P.
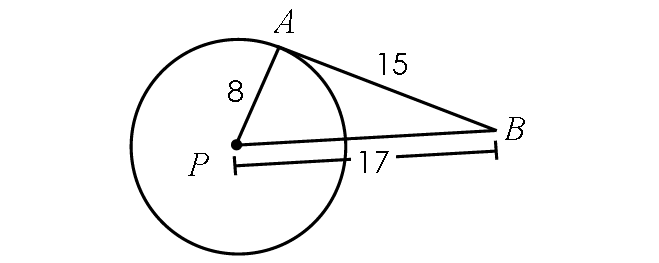
Problem 2 :
Determine if the line segment YX is tangent to circle P.
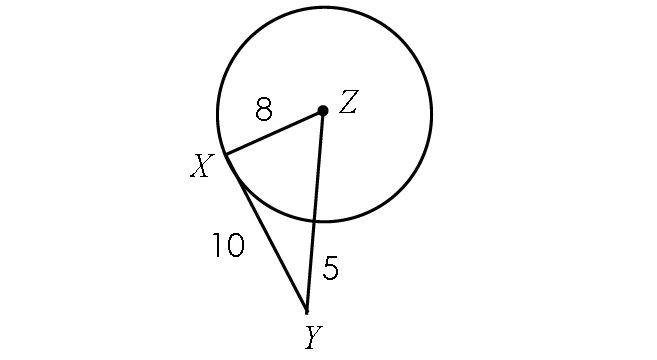
Problem 3 :
If the line segment JK is tangent to circle L, find x.
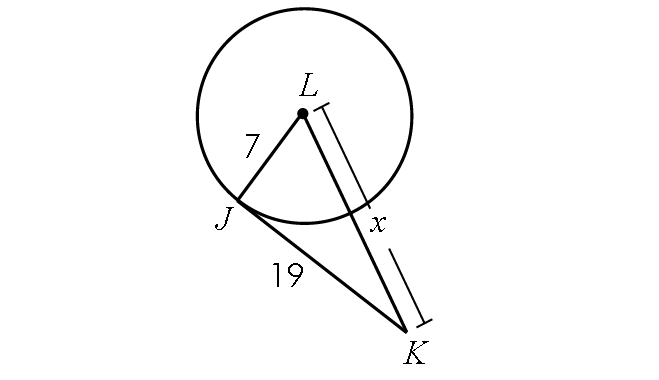
Problem 4 :
If the line segment JK is tangent to circle L, find x.
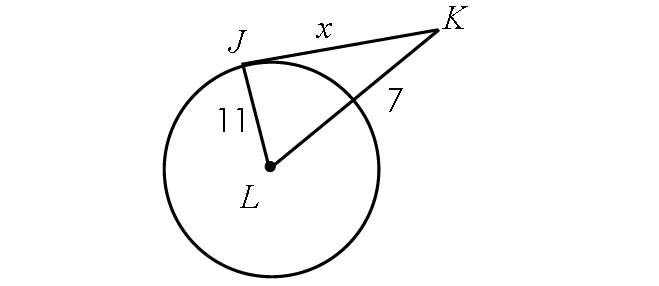
Problem 5 :
If the line segment JK is tangent to circle L, find x.
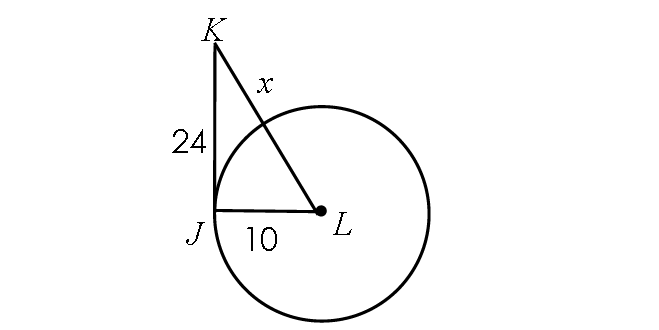
Problem 6 :
If the line segment JK is tangent to circle L, find x.
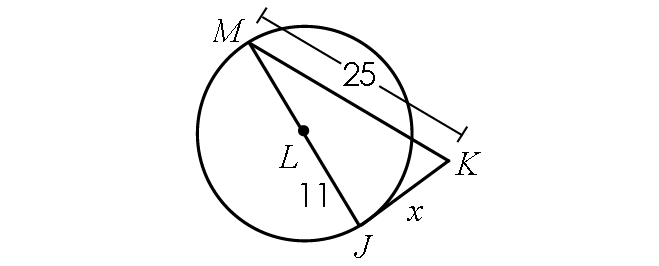
Problem 7 :
If the line segment JK is tangent to circle L, find x.
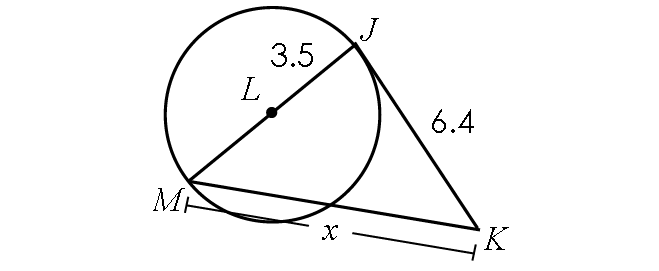
Problem 8 :
If the line segment JK is tangent to circle L, find x.
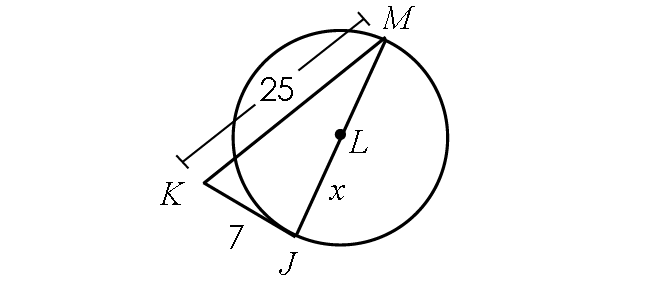
Problem 9 :
If the line segment JK is tangent to circle L, find x.
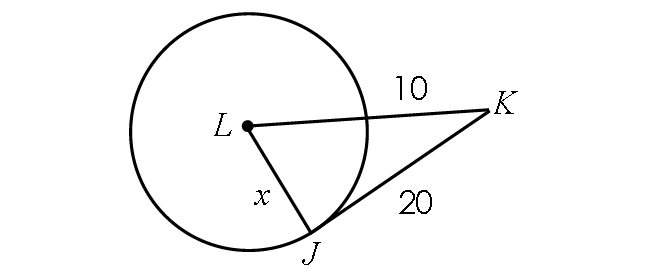
Problem 10 :
Find the value of x. Assume that segment that appears to be tangent is tangent.
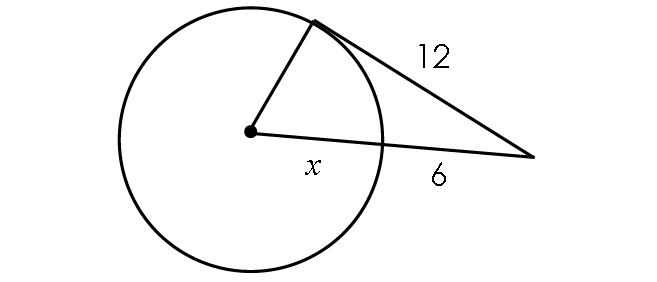

Answers
1. Answer :

If the line segment AB is tangent to circle P, it is perpendicular to the radius PA.
Then, m∠PAB = 90° and triangle PAB has to be a right triangle.
Using Pythagorean Theorem, verify whether triangle PAB is a right triangle.
PA2 + PB2 = PB2
82 + 152 = 172 ?
64 + 225 = 289 ?
289 = 289 ?
The above result is true.
So, triangle PAB is a right triangle and m∠PAB = 90°.
Hence, the line segment AB is tangent to circle P.
2. Answer :
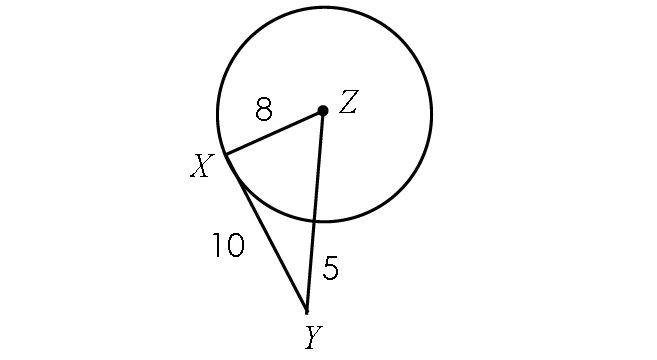
Find the length of ZY :
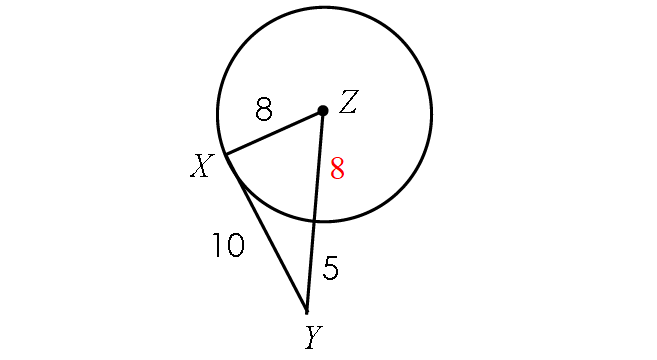
ZY = Radius + 5
ZY = 8 + 5
ZY = 13
If the line segment YX is tangent to circle Z, it is perpendicular to the radius ZX.
Then, m∠ZXY = 90° and triangle ZXY has to be a right triangle.
Using Pythagorean Theorem, verify whether triangle ZXY is a right triangle.
ZX2 + XY2 = ZY2
82 + 102 = 132 ?
64 + 100 = 169 ?
164 = 169 ?
The above result is false.
So, triangle ZXY is not a right triangle and m∠ZXY ≠ 90°.
Hence, the line segment YX is not tangent to circle Z.
3. Answer :
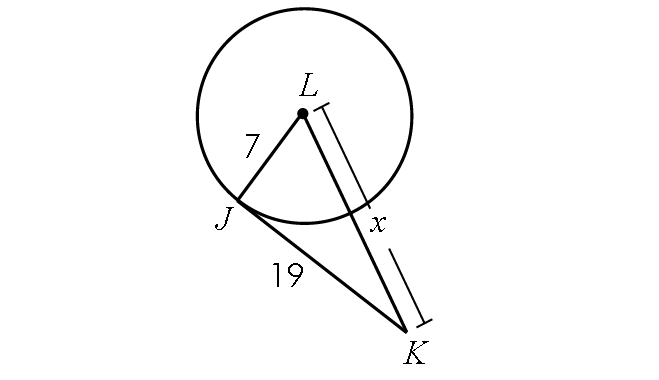
Because JK is tangent to circle L, m∠LJK = 90° and triangle LJK is a right triangle.
BY Pythagorean Theorem,
LJ2 + JK2 = LK2
72 + 192 = x2
49 + 361 = x2
49 + 361 = x2
400 = x2
Take square root on both sides.
20 = x
4. Answer :
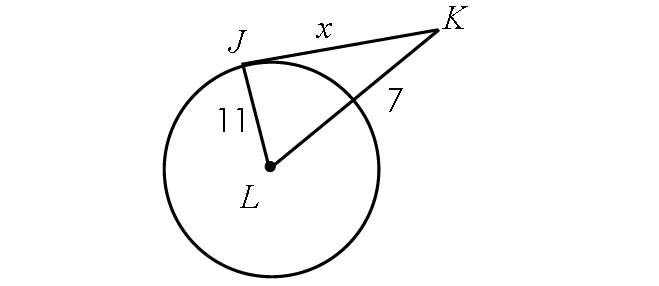
Find the length of LK :
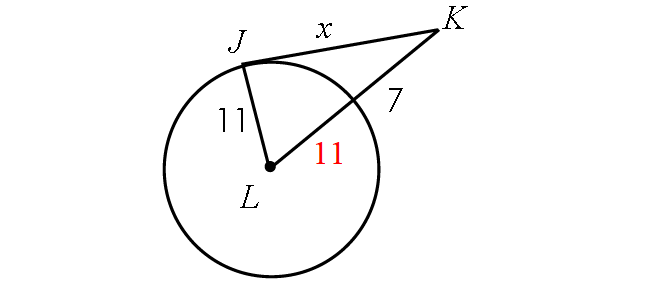
LK = Radius + 7
LK = 11 + 7
LK = 18
Because JK is tangent to circle L, m∠LJK = 90° and triangle LJK is a right triangle.
BY Pythagorean Theorem,
LJ2 + JK2 = LK2
112 + x2 = 182
121 + x2 = 324
Subtract 121 from each side.
x2 = 203
Take square root on both sides.
x ≈ 14.2
5. Answer :
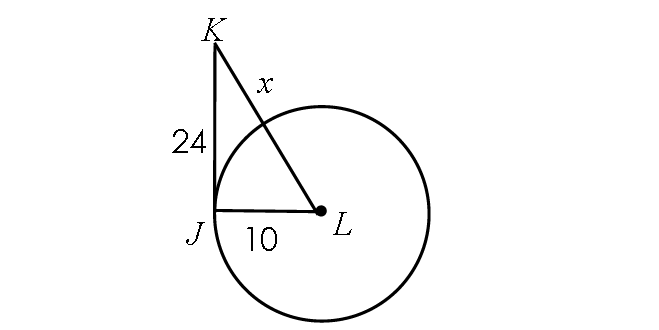
Find the length of LK :
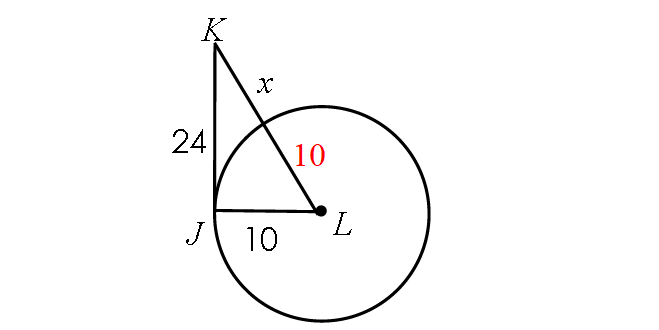
LK = Radius + x
LK = 10 + x
Because JK is tangent to circle L, m∠LJK = 90° and triangle LJK is a right triangle.
BY Pythagorean Theorem,
LJ2 + JK2 = LK2
102 + 242 = (10 + x)2
676 = (10 + x)2
Take square root on both sides.
26 = 10 + x
Subtract 10 from each side.
16 = x
6. Answer :
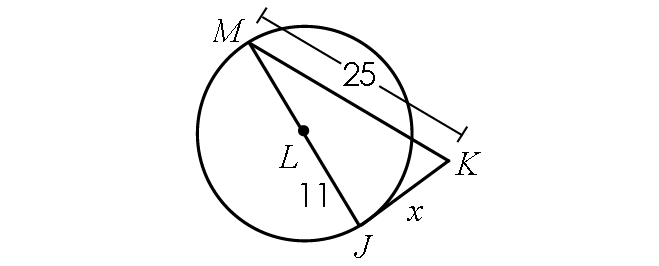
Find the length of JM :
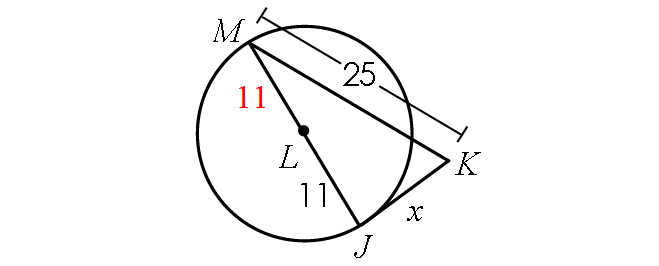
JM = JL + LM
JM = 11 + 11
JM = 22
Because JK is tangent to circle L, m∠MJK = 90° and triangle MJK is a right triangle.
BY Pythagorean Theorem,
JM2 + JK2 = MK2
222 + x2 = 252
484 + x2 = 625
Subtract 484 from each side.
x2 = 141
Take square root on both sides.
x ≈ 11.9
7. Answer :
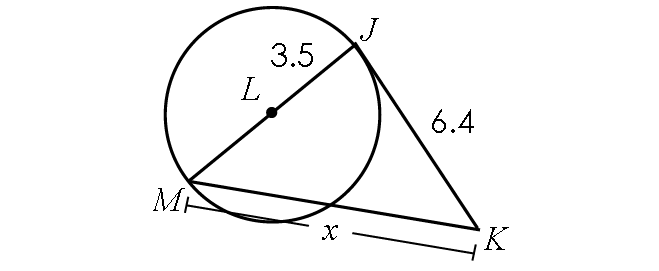
Find the length of JM :
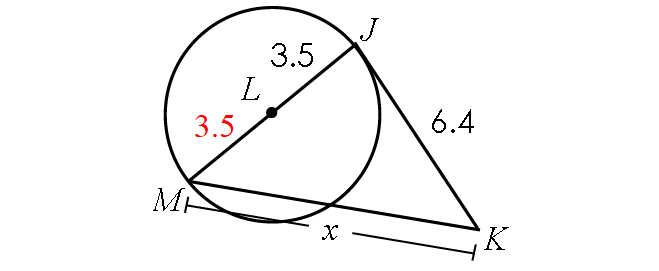
JM = JL + LM
JM = 3.5 + 3.5
JM = 7
Because JK is tangent to circle L, m∠MJK = 90° and triangle MJK is a right triangle.
BY Pythagorean Theorem,
JM2 + JK2 = MK2
72 + 6.42 = x2
49 + 40.96 = x2
89.96 = x2
Take square root on both sides.
9.5 ≈ x
8. Answer :
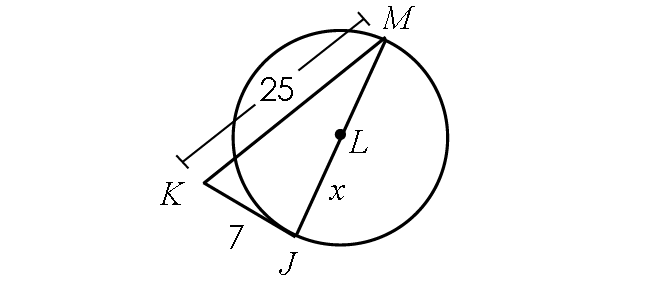
Find the length of JM :
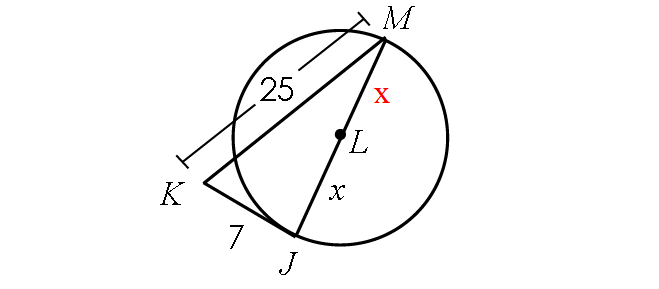
JM = JL + LM
JM = x + x
JM = 2x
Because JK is tangent to circle L, m∠MJK = 90° and triangle MJK is a right triangle.
BY Pythagorean Theorem,
JK2 + JM2 = KM2
72 + (2x)2 = 252
49 + 4x2 = 625
Subtract 49 from each side.
4x2 = 576
Divide each side by 4.
x2 = 144
Take square root on both sides.
x = 12
9. Answer :
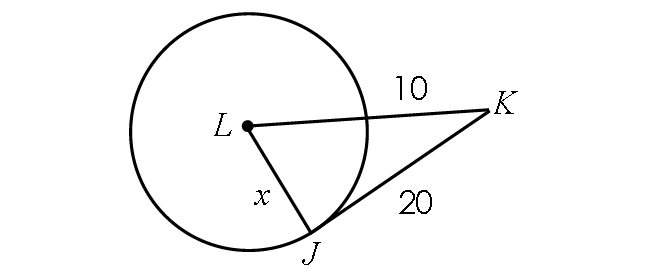
Find the length of LK :
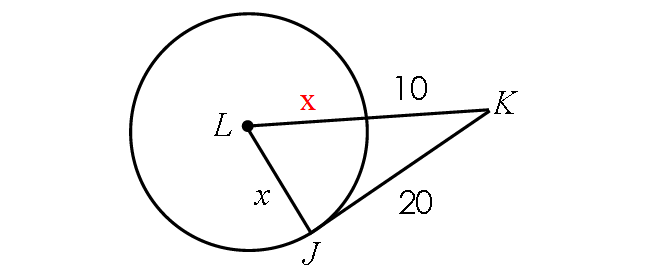
LK = Radius + 10
LK = x + 10
Because JK is tangent to circle L, m∠LJK = 90° and triangle LJK is a right triangle.
BY Pythagorean Theorem,
LJ2 + JK2 = LK2
x2 + 202 = (x + 10)2
x2 + 400 = x2 + 2(x)(10) + 102
x2 + 400 = x2 + 20x + 100
Subtract x2 from each side.
400 = 20x + 100
Subtract 100 from each side.
300 = 20x
Divide each side by 20.
15 = x
10. Answer :
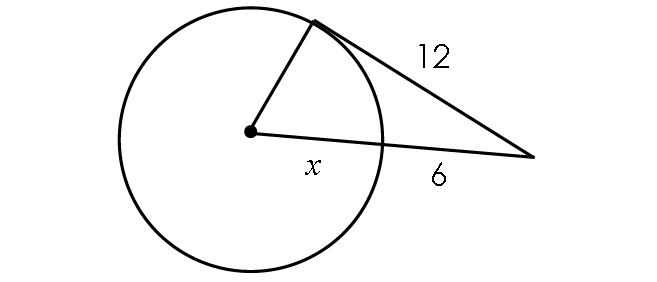
In the diagram above, the length of the missing leg of the triangle is x. Because its the radius of the circle.
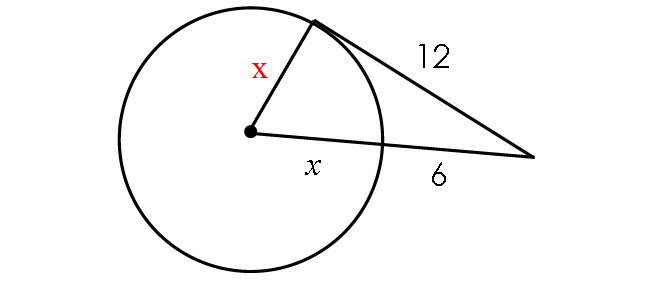
Since the line segment that appears to be tangent is tangent, the triangle is a right triangle.
By Pythagorean Theorem,
x2 + 122 = (x + 6)2
x2 + 144 = x2 + 2(x)(6) + 62
x2 + 144 = x2 + 12x + 36
Subtract x2 from each side.
144 = 12x + 36
Subtract 36 from each side.
108 = 12x
Divide each side by 12.
9 = x
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
10 Hard SAT Math Questions (Part - 33)
Nov 07, 25 04:31 AM
10 Hard SAT Math Questions (Part - 33) -
Solving the HARDEST SAT Math Questions ONLY using Desmos
Nov 04, 25 07:33 AM
Solving the HARDEST SAT Math Questions ONLY using Desmos -
10 Hard SAT Math Questions (Part - 32)
Oct 30, 25 08:57 AM
10 Hard SAT Math Questions (Part - 32)
