TESTING CONTINUITY OF A FUNCTION WORKSHEET WITH ANSWERS

(1)  Prove that f(x) = 2x² + 3x - 5 is continuous at all points in R.    Solution

(2)  Examine the continuity of the following 

(i)  x + sin x       Solution

(ii)  x² cos x        Solution

(iii)  e^x tan x       Solution

(iv)  e^2x + x^{2             Solution}

(v)  x ln x          Solution

(vi)  sin x / x^{2        Solution}

(vii)  (x² - 16) / (x + 4)       Solution

(viii)  |x + 2| + |x - 1|      Solution

(ix)  |x - 2| / |x + 1|      Solution

(x)  cot x + tan x        Solution

(3)  Find the points of discontinuity of the function f, where

Solution

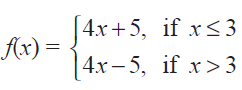
(ii)

Solution

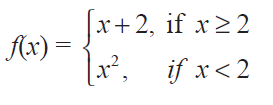
(iii)

Solution

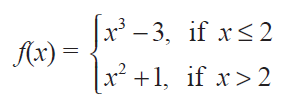
(iv)

Solution

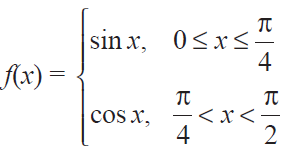
(4)  At the given point x₀ discover whether the given function is continuous or discontinuous citing the reasons for your answer :

Solution

Solution

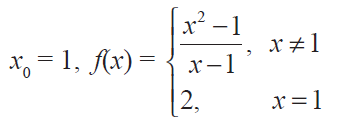
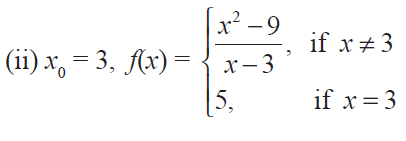
(5)  Show that the function

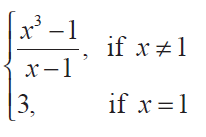
is continuous on (- ∞, ∞).        Solution

(6)  For what value of a is this function f(x) = 

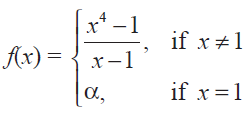
continuous at x = 1 ?      Solution

(7)  Let f(x)

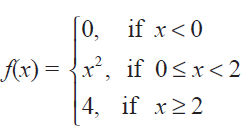
Graph the function. Show that f(x) continuous on (- ∞, ∞).

Solution

(8)  If f and g are continuous functions with f(3) = 5 and lim x->3 [2 f(x) - g(x)]  =  4, find g(3).       Solution

(9)  Find the points at which f is discontinuous. At which of these points f is continuous from the right, from the left, or neither? Sketch the graph of f.

Solution

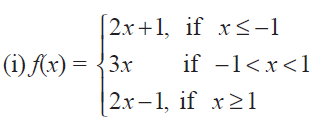
(10)  A function f is defined as follows :

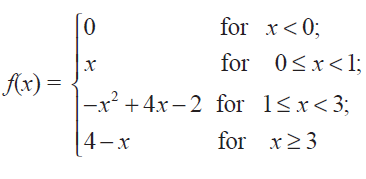
Is the function continuous?

(11)  Which of the following functions f has a removable discontinuity at x = x₀? If the discontinuity is removable, find a function g that agrees with f for x ≠ x₀ and is continuous on R.

(i)  f(x)  =  (x² - 2x - 8)/(x + 2), x₀  =  -2      Solution

(ii)  f(x)  =  (x³ + 64)/(x + 4), x₀  =  -4       Solution

(iii)  f(x)  =  (3 - √x)/(9 - x), x₀  =  9        Solution

(12)  Find the constant b that makes g continuous on (−∞, ∞)

Solution

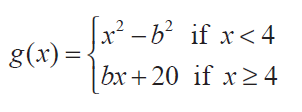
(13)  Consider the function f (x) = x sin π/x What value must we give f(0) in order to make the function continuous everywhere?        Solution

(14)  The function f(x)  =  (x² - 1) / (x³ - 1) is not defined at x = 1. What value must we give f(1) inorder to make f(x) continuous at x = 1 ?       Solution

(15)  State how continuity is destroyed at x = x₀ for each of the following graphs.

(i)  

Solution

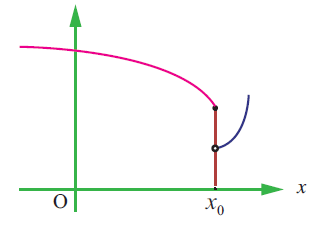
(ii)  

Solution

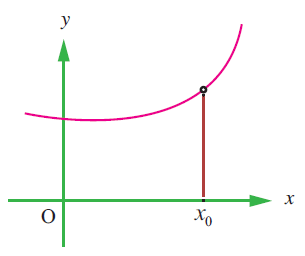
(iii)

Solution

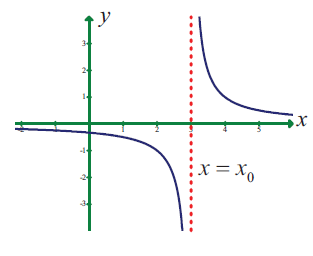
(iv)

Solution

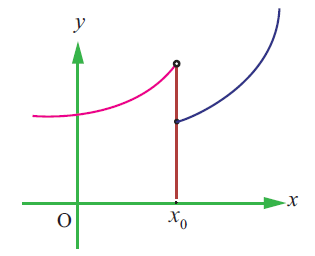
Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.