TESTING FOR SYMMETRY WORKSHEET

Problems 1-3 : Graphically determine what type(s) of symmetry, if any, are present.

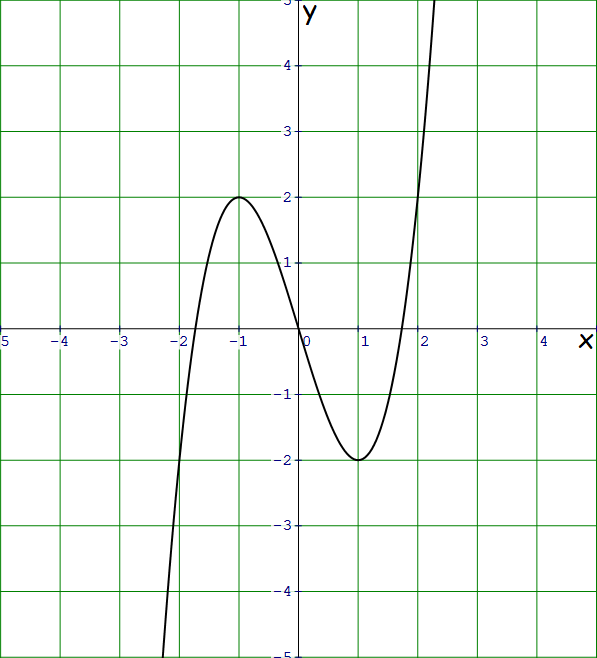
Problem 1 :

Problem 2 :

Problem 3 :

Problems 4-6 : Algebraically check for symmetry with respect to the x-axis, y-axis, and the origin.

Problem 4 :

y = x² + 4

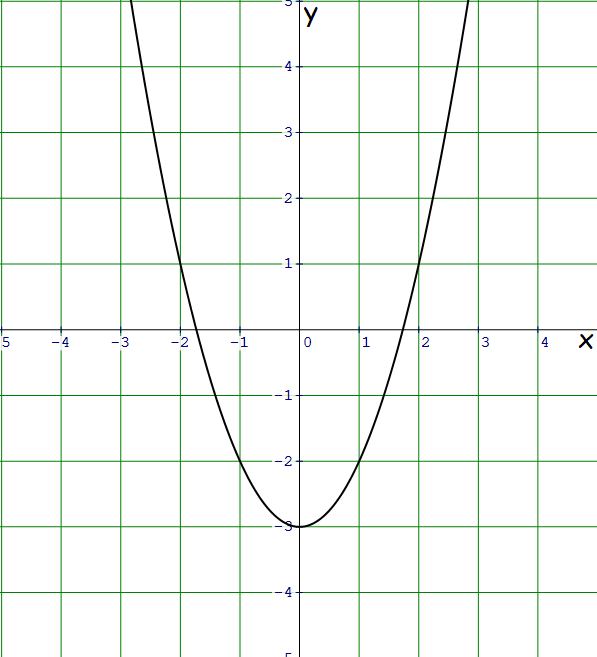
Problem 5 :

y = x³

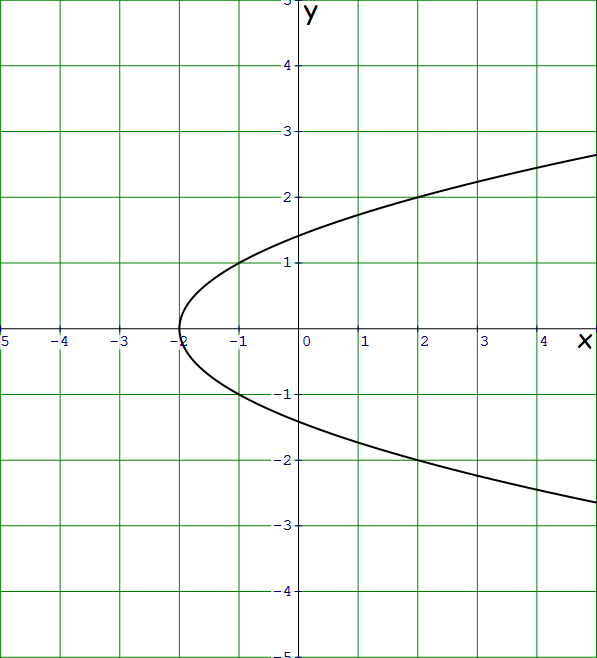
Problem 6 :

x = y² + 5

Problem 7 :

x² + y² = 36

Problem 8 :

y = |x| - 2

1. Solution :

Plot some random points on the graph.

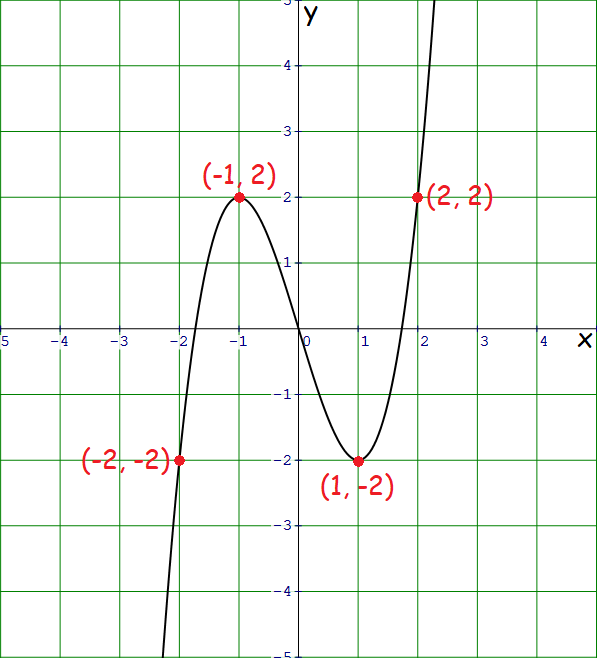
Consider the following pairs of points on the graph.

(-1, 2) and (1, -2)

(-2, -2) and (2, -2)

From the above pairs of points on the graph, it is clear that if (x, y) is on the graph, then (-x, -y) is also on the graph.

Hence, the graph is symmetric with respect to the origin.

2. Solution :

Plot some random points on the graph.

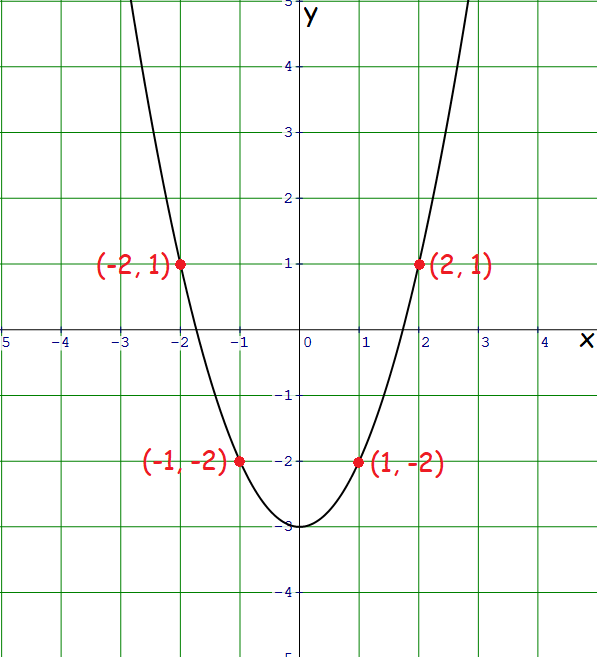
Consider the following pairs of points on the graph.

(-1, -2) and (1, -2)

(-2, 1) and (2, 1)

From the above pairs of points on the graph, it is clear that if (x, y) is on the graph, then (-x, y) is also on the graph.

Hence, the graph is symmetric with respect to the y-axis.

3. Solution :

Plot some random points on the graph.

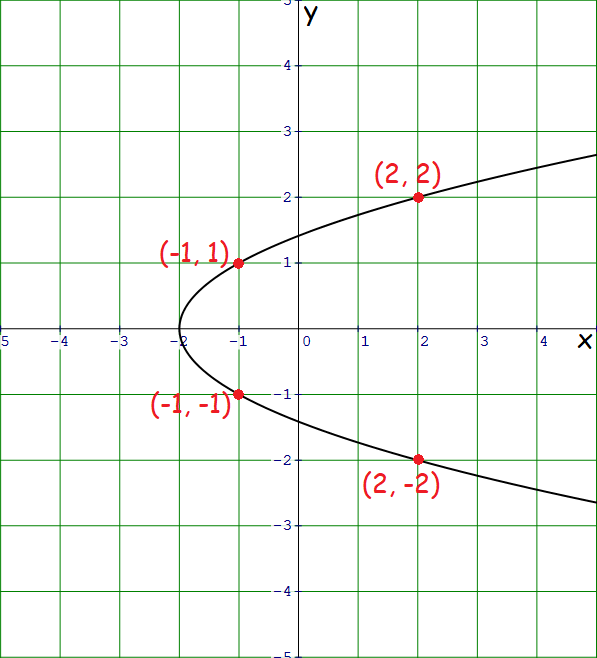
Consider the following pairs of points on the graph.

(-1, -1) and (-1, 1)

(2, -2) and (2, 2)

From the above pairs of points on the graph, it is clear that if (x, y) is on the graph, then (x, -y) is also on the graph.

Hence, the graph is symmetric with respect to the x-axis.

4. Solution :

y = x² + 4

In the given equation, y = x² + 4, the power of x is even and the power of y is odd.

Since the power of x is even, replacing x by -x may unalter the original equation.

Check :

y = x² + 4

y = (-x)² + 4

y = x² + 4

In the given equation, when 'x' is replaced by '-x', the equation is unaltered.

Hence, the graph of the given equation is symmetric with respect to the y-axis.

5 Solution :

In the given equation y = x³, both the powers of x and y are odd.

Since both the powers of x and y are odd, replacing x by -x and y by -y may unalter the original equation.

Check :

y = x³

Replace x by -x and y by -y.

-y = (-x)³

-y = -x³

Multiply both sides by -1.

y = x³

In the given equation, when x is replaced by -x and y is replaced by -y, the equation is unaltered.

Hence, the graph of the given equation is symmetric with respect to the origin.

6. Solution :

In the given equation, x = y² + 5, the power of x is odd and the power of y is even.

Since the power of y is even, replacing y by -y may unalter the original equation.

Check :

x = y² + 5

x = (-y)² + 5

x = y² + 5

In the given equation, when 'y' is replaced by '-y', the equation is unaltered.

Hence, the graph of the given equation is symmetric with respect to the x-axis.

7. Solution :

In the given equation, x² + y² = 4, both the powers of x and y are even.

Since the power of y is even, replacing y by -y may unalter the original equation.

Since the power of x is even, replacing x by -x may unalter the original equation.

Since both the powers of x and y are even, replacing x by -x and y by -y may unalter the original equation.

In all the three cases, the original equation is unaltered.

The graph of the given equation is symmetric with respect to the x-axis, the y-axis and the origin.

8. Solution :

In the given equation y = |x| - 2, there is absolute value of x.

Since 'x' is in absolute value, replacing x by -x may unalter the equation.

Check :

y = |x| - 2

Replace x by -x.

y = |-x| - 2

y = |x| - 2

In the given equation, when 'x' is replaced by '-x', the equation is unaltered.

Hence, the graph of the given equation is symmetric with respect to the y-axis.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.