THE PYTHAGOREAN THEOREM WORKSHEET

Problem 1 :

Find the length of the hypotenuse of the right triangle shown below. Tell whether the side lengths form a Pythagorean triple.

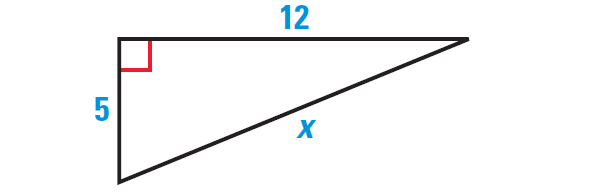
Problem 2 :

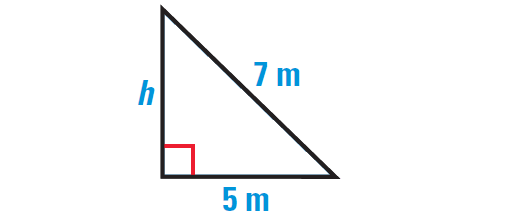
Find the length of the leg of the right triangle shown below. 

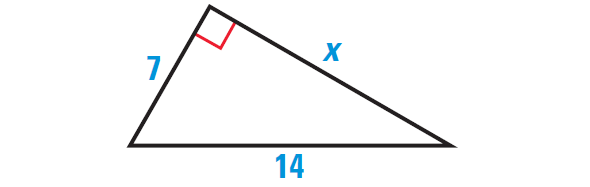
Problem 3 : 

Find the area of the triangle to the nearest tenth of a meter.

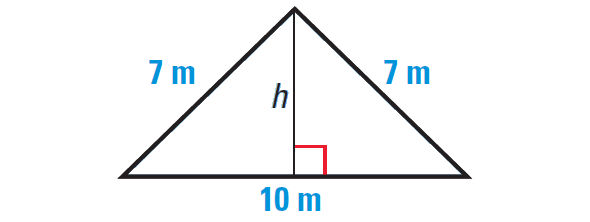
Example 4 :

The figure shows a right triangle. Find the approximate length of the hypotenuse to the nearest tenth. Check your answer for reasonableness.

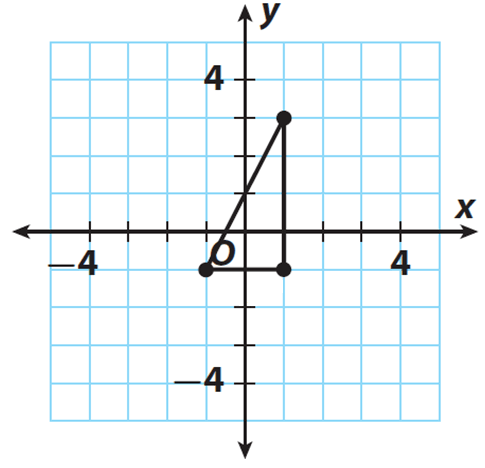
Problem 5 :

One of the diagonals of a rectangle is 20 cm long. If the difference between its length and width is 4 cm, then find the length and width of the rectangle.

Problem 6 : 

A box used for shipping narrow silver sticks measures 6 inches by 6 inches by 20 inches. What is the length of the longest stick that will fit in the box, given that the length of the tube must be a whole number of inches?

Problem 7 :

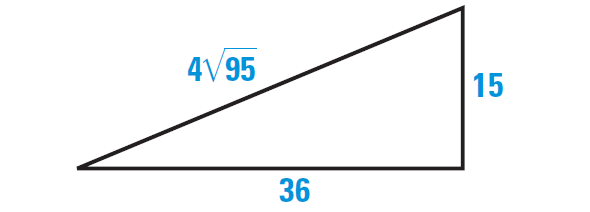
The triangle shown below appears to be a right triangle. Say whether it is right a triangle.

Problem 8 :

A rhombus has diagonals of length 6 cm and 8 cm. Find the length of its sides.

Answers

1. Answer :

By Pythagorean Theorem, we have

(Hypotenuse)²  =  (leg)² + (leg)²

Substitute.

x²  =  5² + 12²

Simplify.

x²  =  25 + 144

x²  =  169

Take square root on each side.

√x²  =  √169

x  =  13

So, the length of the hypotenuse is 13 units. 

Because 13²  =  12² + 5², they form a Pythagorean triple. 

2. Answer :

By Pythagorean Theorem, we have

(Hypotenuse)²  =  (leg)² + (leg)²

Substitute.

14²  =  7² + x²

Simplify.

196  =  49 + x²

Subtract 49 from each side. 

147  =  x²

Take square root on each side.

√147  =  √x²

√147  =  x

Use product property.

√49 ⋅ √3  =  x

Simplify the radical. 

7√3  =  x 

Hence, the required side length is 7√3 units. 

3. Answer :

We are given that the base of the triangle is 10 meters, but we do not know the height h.

Because the triangle is isosceles, it can be divided into two congruent right triangles with the given dimensions. Use the Pythagorean Theorem to find the value of h.

By Pythagorean Theorem, we have

7²  =  5² + h²

Simplify.

49  =  25 + h²

Subtract 25 from each side.

24  =  h²

Take square root on each side.

√24  =  √h²

√24  =  h

Now find the area of the original triangle. 

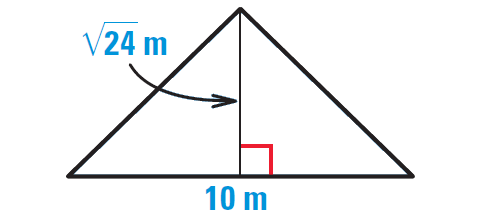
Area  =  1/2 ⋅ b ⋅ h

Substitute.

Area  =  1/2 ⋅ 10 ⋅ √24

Use calculator to approximate. 

Area  =  1/2 ⋅ 10 ⋅ √24

Area  ≈  24.5 m²

Hence, the area of the triangle is about 24.5 m².

4. Answer :

Step 1 :

Find the length of each leg.

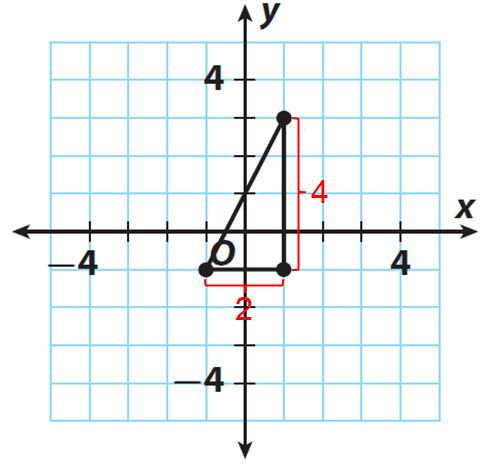
The length of the vertical leg is 4 units.

The length of the horizontal leg is 2 units. 

Step 2 :

Let a = 4 and b = 2 and c represent the length of the hypotenuse.

Because a and b are legs and c is hypotenuse, by Pythagorean Theorem, we have

a² + b²  =  c²

Step 3 :

Substitute a = 4 and b = 2 in (a² + b²  =  c²⁾ to solve for c. 

4² + 2²  =  c²

Simplify.

16 + 4  =  c²

20  =  c²

Take the square root of both sides.

√20  =  √c²

√20  =  c

Step 4 :

Find the value of √20 using calculator and round to the nearest tenth

4.5  ≈  c

Step 5 :

Check for reasonableness by finding perfect squares close to 20.

√20 is between √16 and √25, so 4 < √20 < 5.

Since 4.5 is between 4 and 5, the answer is reasonable.

The hypotenuse is about 4.5 units long.

5. Answer :

Let x be the length of the rectangle. 

Since the difference between the length and width is 4 cm, the width of the rectangle has to be either (x + 4) cm or (x - 4) cm.

We can take the width of the rectangle as (x + 4) cm.

Draw a sketch. 

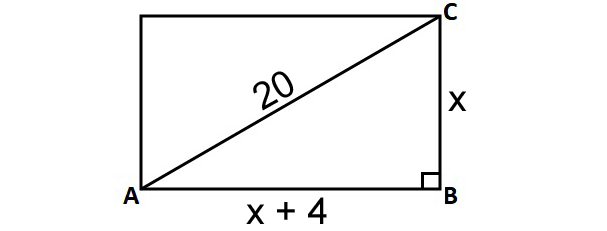
In the picture above, consider the right triangle ABC.

By The Pythagorean Theorem, 

x² + (x + 4)²  =  20²

x² + (x + 4)(x + 4)  =  400

x² + x² + 4x + 4x + 16  =  400

2x² + 8x + 16  =  400

Subtract 400 from each side. 

2x² + 8x - 384  =  0

Divide both sides by 2. 

x² + 4x - 192  =  0

Factor and solve.

(x + 16)(x - 12)  =  0

x + 16 = 0     or     x - 12 = 0

x = -16     or     x = 12

Since the length of a rectangle can never be a negative value, we can ignore x = -16. 

So, the value of x is 12.

Then, 

x + 4  =  12 + 4

x + 4  =  16

Therefore,

length  =  12 cm 

width  =  16 cm

6. Answer :

Step 1 : 

Draw an appropriate diagram for the given information.

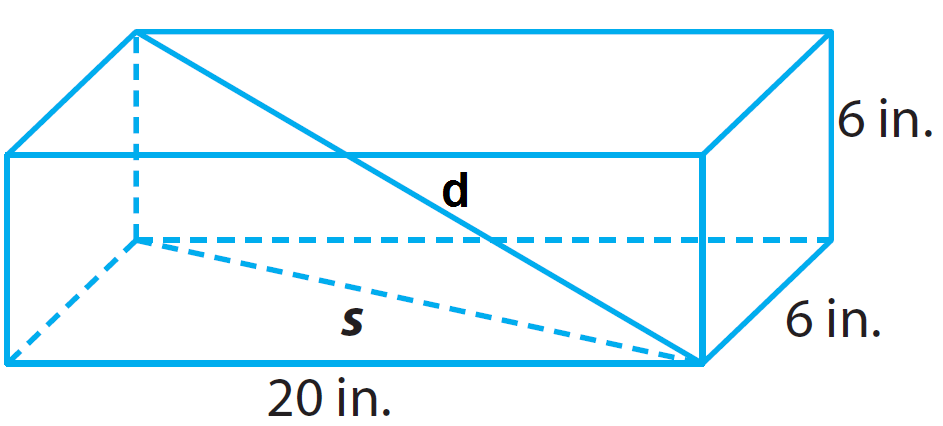
From the diagram given above, the box has the following dimensions.

Length (l)  =  20 in.

Width (w)  =  6 in.

Height (h)  =  6 in.

Step 2 :

We want to find d, the length from a bottom corner to the opposite top corner.

Using The Pythagorean Theorem, find s, the length of the diagonal across the bottom of the box.

w² + l²  =  s²

Step 3 :

Substitute the given measures.

6² + 20²  =  s²

Simplify.

36 + 400  =  s²

436  =  s²

Step 3 :

Use the expression for s to find d.

h² + s²  =  d²

Step 4 :

Plug h = 6 and s² = 436. 

6² + 436  =  d²

Simplify.

36 + 436  =  d²

472  =  d²

Take square root on both sides.

√472  =  √d²

21.7  ≈  d

Hence, the length of the longest stick that will fit in the box is 21 inches.

7. Answer :

Let c represent the length of the longest side of the triangle. Check to see whether the side lengths satisfy the equation

c²  =  a² + b²

Substitute.

 (4√95)²  =  15² + 36²  ?

 4² ⋅ (√95)²  =  15² + 36²  ?

16 ⋅ 95  =  225 + 1296  ?

 1520  ≠  1521

Because the lengths of the sides of the triangle do not satisfy the equation c² = a² + b², the triangle shown above is not a right triangle. 

8. Answer :

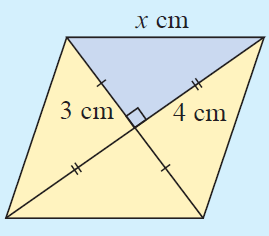
In rhombus, the diagonals will intersect each other at 90 degree.

We have four right triangles inside the rhombus above.

Using The Pythagorean Theorem in one of the right triangles,

x²  =  3² + 4²

x²  =  9 + 16

x²  =  25

x  =  √25

x  =  5

So, the side length of rhombus is 5 cm.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.