THE SLOPE FORMULA WORKSHEET
Problem 1 :
Find the slope of the line that contains (5, -3) and (-2, 3).
Problem 2 :
Find the slope of the line that contains (-2, -2) and (7, -2).
Problem 3 :
A line passes through the points (3/4, 7/5) and (1/4, 2/5). Find its slope.
Problem 4-5 : Each graph shows a linear relationship. Find the slope.
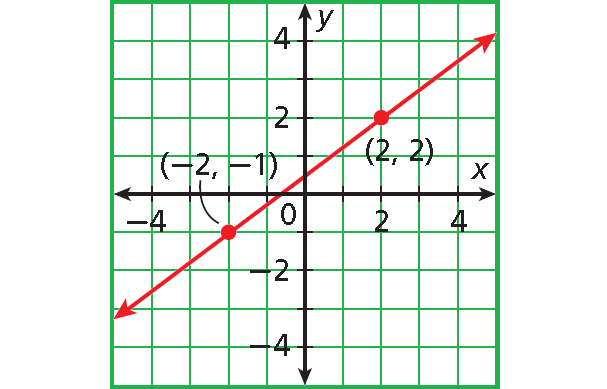
Problem 4 :
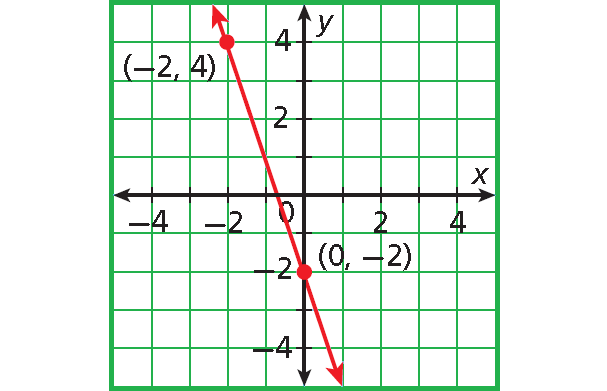
Problem 5 :
Problem 6-7 : Each table shows a linear relationship. Find the slope
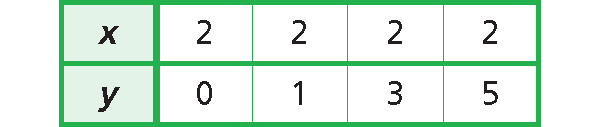
Problem 6 :
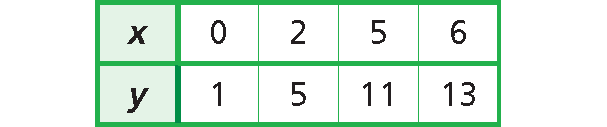
Problem 7 :
Problem 8 :
Find the slope of the line described by 6x - 5y = 30.
Problem 9 :
Find the slope of the line described by 2x + 3y = 12.
Problem 10 :
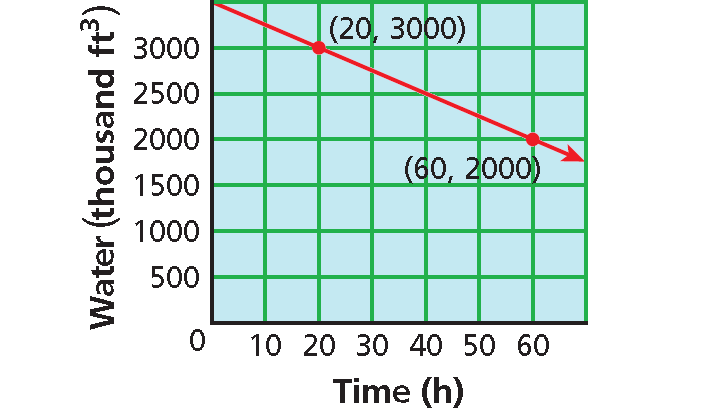
The graph shows how much water is in a reservoir at different times. Find the slope of the line. Explain what the slope represents.

Detailed Answer Key
1. Answer :
Use the slope formula.
m = (y2 - y1)/(x2 - x1)
Substitute (4, -2) for (x1 , y1) and (-1, 2) for (x2, y2).
m = [3 - (-3)]/(-2 - 5)
m = (3 + 3)/(-7)
m = 6/(-7)
m = -6/7
The slope of the line that contains (5, -3) and (-2, 3) is -6/7.
2. Answer :
Use the slope formula.
m = (y2 - y1)/(x2 - x1)
Substitute (-2, -2) for (x1 , y1) and (7, -2) for (x2, y2).
m = [-2 - (-2)]/[7 - (-2)]
m = (-2 + 2)/(7 + 2)
m = 0/9
m = 0
The slope of the line that contains (-2, -2) and (7, -2) is 0.
3. Answer :
Use the slope formula.
m = (y2 - y1)/(x2 - x1)
Here,
(x1 , y1) = (3/4, 7/5)
(x2, y2) = (1/4, 2/5)
Then,
m = (2/5 - 7/5)/(1/4 - 3/4)
m = (-5/5) / (-2/4)
m = (-1) / (-1/2)
m = (-1)(-2/1)
m = 2
The slope of the line that contains (-2, -2) and (7, -2) is 0.
4. Answer :
Let (-2, -1) be (x1, y1) and (2, 2) be (x2 , y2).
Use the slope formula.
m = (y2 - y1)/(x2 - x1)
Substitute (-2, -1) for (x1 , y1) and (2, 2) for (x2, y2).
m = [2 - (-1)]/[2 - (-2)]
m = (2 + 1)/(2 + 2)
m = 3/4
The slope of the line is 3/4.
5. Answer :
Let (-2, 4) be (x1, y1) and (0, -2) be (x2 , y2).
Use the slope formula.
m = (y2 - y1)/(x2 - x1)
Substitute (-2, 4) for (x1 , y1) and (0, -2) for (x2, y2).
m = (-2 - 4)/[0 - (-2)]
m = -6/(0 + 2)
m = -6/2
m = -3
The slope of the line is -3.
6. Answer :
Choose any two points from the table.
Let (2, 0) be (x1, y1) and (2, 3) be (x2 , y2).
Use the slope formula.
m = (y2 - y1)/(x2 - x1)
Substitute (2, 0) for (x1 , y1) and (2, 3) for (x2, y2).
m = (3 - 0)/(2 - 2)
m = 3/0
m = Undefined
The slope is undefined.
7. Answer :
Choose any two points from the table.
Let (0, 1) be (x1, y1) and (5, 11) be (x2 , y2).
Use the slope formula.
m = (y2 - y1)/(x2 - x1)
Substitute (0, 1) for (x1 , y1) and (5, 11) for (x2, y2).
m = (11 - 1)/(5 - 0)
m = 10/5
m = 2
The slope is 2.
8. Answer :
|
Find the x-intercept : 6x - 5y = 30 6x - 5(0) = 30 6x - 0 = 30 6x = 30 x = 5 (5, 0) |
Find the y-intercept : 6x - 5y = 30 6(0) - 5y = 30 0 - 5y = 30 -5y = 30 y = -6 (0, -6) |
The line contains (5, 0) and (0, -6). Use the slope formula.
Use the slope formula.
m = (y2 - y1)/(x2 - x1)
Substitute (5, 0) for (x1 , y1) and (0, -6) for (x2, y2).
m = (-6 - 0)/(0 - 5)
m = -6/(-5)
m = 6/5
The slope is 6/5.
9. Answer :
|
Find the x-intercept : 2x + 3y = 12 2x + 3(0) = 12 2x + 0 = 12 2x = 12 x = 6 (6, 0) |
Find the y-intercept : 2x + 3y = 12 2(0) + 3y = 12 0 + 3y = 12 3y = 12 y = 4 (0, 4) |
The line contains (6, 0) and (0, 4). Use the slope formula.
Use the slope formula.
m = (y2 - y1)/(x2 - x1)
Substitute (6, 0) for (x1 , y1) and (0, 4) for (x2, y2).
m = (4 - 0)/(0 - 6)
m = 4/(-6)
m = -4/6
m = -2/3
The slope is -2/3.
10. Answer :
Use the slope formula.
m = (y2 - y1)/(x2 - x1)
Here,
(x1 , y1) = (20, 3000)
(x2, y2) = (60, 2000)
Then,
m = (2000 - 3000)/(60 - 20)
m = -1000/40
m = -25
The slope is -25.
In the given situation, y represents volume of water and x represents time.
So slope represents
change in volume/change in time
in units of
thousands of cubic feet/hours.
A slope of -25 means the amount of water in the reservoir is decreasing (negative change) at a rate of 25 thousand cubic feet each hour.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
SAT Math Resources (Videos, Concepts, Worksheets and More)
Feb 08, 25 10:15 PM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Digital SAT Math Problems and Solutions (Part - 107)
Feb 08, 25 10:13 PM
Digital SAT Math Problems and Solutions (Part - 107) -
Digital SAT Math Problems and Solutions (Part - 108)
Feb 08, 25 10:09 PM
Digital SAT Math Problems and Solutions (Part - 108)