THEORY PROBLEMS AND SOLUTIONS IN VECTOR

Question 1 :

If D and E are the midpoints of the sides AB and AC of a triangle ABC, prove that BE vector + DC vector = (3/2) BC vector.

Solution :

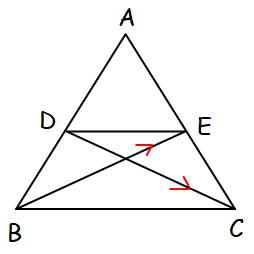
OA vector  =  a vector,

OB vector  =  b vector,

OC vector =  c vector

Since D is the midpoint of the side AB,

OD vector  =  (a vector + b vector)/2

Since E is the midpoint of the side AC,

OE vector  =  (a vector + c vector)/2

BE vector  =  OE vector - OB vector

= [(a vector + c vector)/2] - b vector

=  (a vector + c vector - 2b vector)/2   ----(1)

DC vector  =  OC vector - OD vector

= c vector - [(a vector + b vector)/2]

=  (2c vector - a vector - b vector)/2  -----(2)

(1) + (2)

  =  (a vector+c vector-2b vector)+(2c vector-a vector-b vector) / 2

  =  (-3b vector + 3c vector) / 2

  =  (3/2) (c vector - b vector)

  =  (3/2) (OC vector - OB vector)

  =  (3/2)  BC vector 

Hence it is proved.

Question 2 :

Prove that the line segment joining the midpoints of two sides of a triangle is parallel to the third side whose length is half of the length of the third side.

Solution :

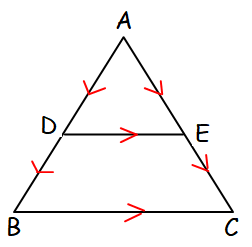
In triangle ADE,

AD vector + DE vector  =  AE vector

DE vector  =  AE vector - AD vector   ---(1)

E is the midpoint of the side AC

So, AE  =  EC

AE  =  (1/2) AC vector

D is the midpoint of the side AB

So, AD  =  DC

AD  =  (1/2) AB vector

By applying the value of AE and AD, we get

DE vector  =  [(1/2) AC vector] - [(1/2) AB vector]

DE vector  =  (1/2) [AC vector - AB vector]  ---(2)

In triangle ABC,

AB vector + BC vector  =  AC vector

  BC vector  =  AC vector - AB vector

By applying the value of BC vector in (2), we get

DE vector  =  (1/2) BC vector

Hence the sides DE and BC are parallel.

Question 3 :

Prove that the line segments joining the midpoints of the adjacent sides of a quadrilateral form a parallelogram.

Solution :

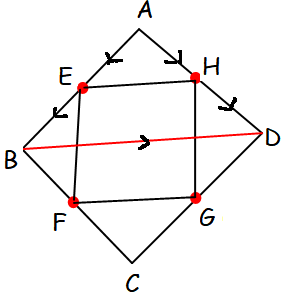
Given : ABCD is a quadrilateral

E, F, G and H are midpoints of the sides AB, BD, DC and CA respectively.

In triangle ABC :

AB vector + BD vector  =  AC vector  ---(1)

In triangle AEH :

AE vector + EH vector  =  AH vector

EH vector  =  AH vector - AE vector

Instead of AH vector, we may write (1/2) AC vector. Instead of AE vector, we may write (1/2) AB vector.

EH vector  =  (1/2) AC vector - (1/2) AB vector

    =  (1/2) [AC vector - AB vector]

From (1), we get 

BD vector  =  AC vector - AB vector

EH vector  =  (1/2) BD vector  ----(A)

Hence we conclude that the sides BD and EH are parallel.

Now, let us consider the triangle BCD and triangle FCG

BC vector + BD vector  =  CD vector  ---(2)

In triangle FCG

FC vector + FG vector  =  CG vector

FG vector  =  CG vector - FC vector

=  (1/2)CD vector - (1/2)BC vector

=  (1/2) [CD vector - BC vector]

From (2),

CD vector - BC vector  =  BD vector

=  (1/2) BD vector-----(B)

From (A) and (B), EFGH is a parallelogram.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.