THIRD ANGLE THEOREM WORKSHEET

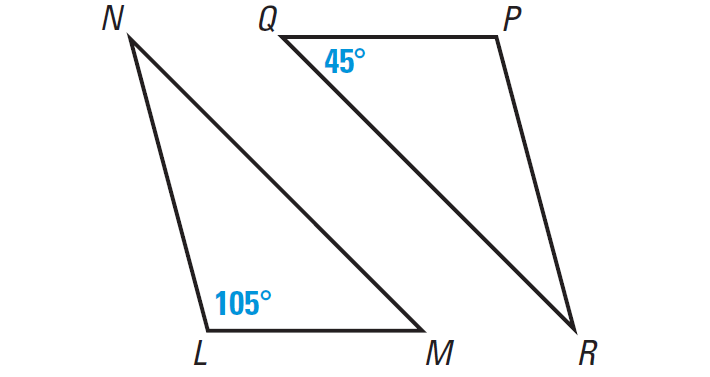
1.  In the diagram shown below, ∠L ≅ ∠P and ∠M ≅ ∠Q, find m∠N and m∠R. Check whether ∠N ≅ ∠R and justify your answer.   

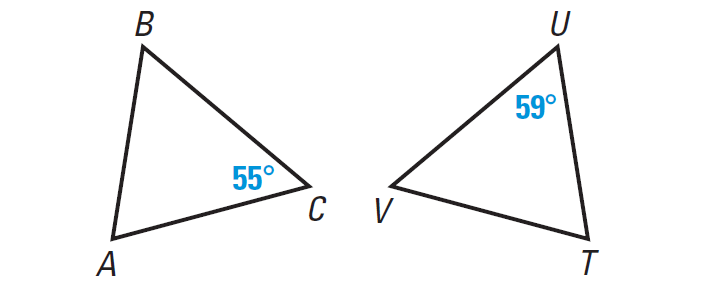
2.  In the diagram given below, ∠B ≅ ∠U and ∠C ≅ ∠V, find m∠A and using the Third Angles Theorem to find m∠T.

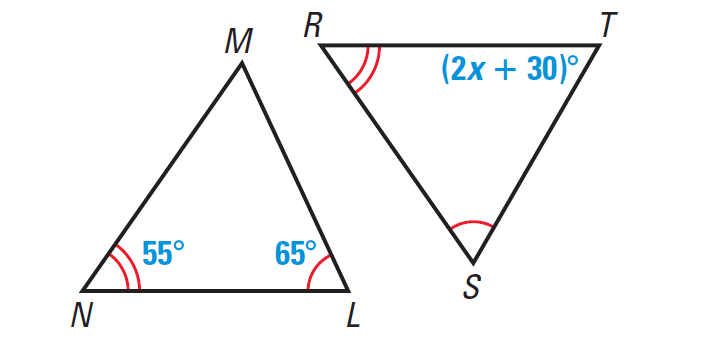
3.  Find the value of x in the diagram given below. 

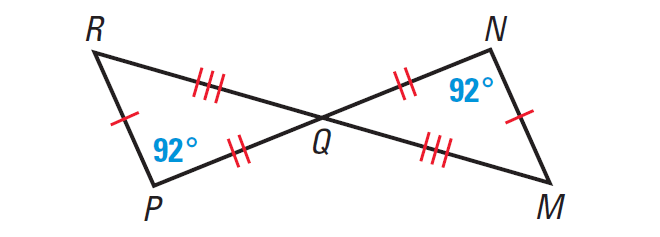
4.  Decide whether the triangles are congruent. Justify your reasoning. 

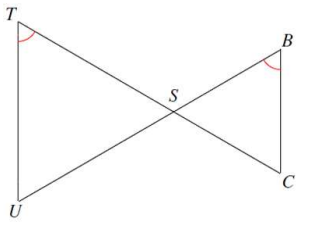
5. Are the triangles in this figure similar? If so, give the reason for similarity and complete the similarity statement below 

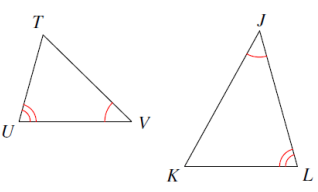
6. Are the triangles in this figure similar? If so, give the reason for similarity and complete the similarity statement below.

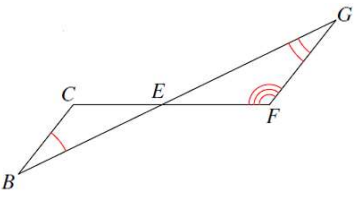
7. Are the triangles in this figure similar? If so, give the reason for similarity and complete the similarity statement below.

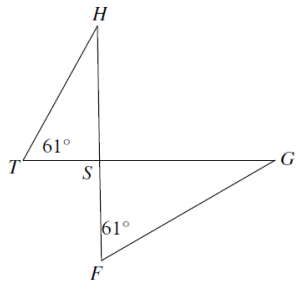
8. Are the triangles in this figure similar? If so, give the reason for similarity and complete the similarity statement below.

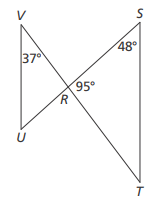
9. Is triangle RST similar to triangle RUV? Explain your reasoning

1. Answer : 

Given : ∠L ≅ ∠P and ∠M ≅ ∠Q.

ΔLMN : 

By the Triangle Sum theorem, we have

m∠L + m∠M + m∠N  =  180°

Substitute 105° for m∠L and 45° for m∠M.

105° + 45° + m∠N  =  180°

Simplify. 

150° + m∠N  =  180°

Subtract 150° from both sides. 

m∠N  =  30°

ΔPQR : 

By the Triangle Sum theorem, we have 

m∠P + m∠Q + m∠R  =  180°

Substitute 105° for m∠P and 45° for m∠Q.

105° + 45° + m∠R  =  180°

Simplify. 

150° + m∠R  =  180°

Subtract 150° from both sides.

m∠R  =  30°

Because m∠N = 30° and m∠R = 30°, we have

m∠N = m∠R -----> ∠N ≅ ∠R

Justification : 

By the Third Angles Theorem, if two angles of one triangle are congruent to two angles of another triangle, then the third angles are also congruent.

So, ∠N ≅ ∠R.

2. Answer : 

Given : ∠B ≅ ∠U and ∠C ≅ ∠V. 

From the figure, we have m∠U = 59°.

Because ∠B ≅ ∠U, we have m∠B = 59°.

In ΔABC, by the Triangle Sum theorem, we have 

m∠A + m∠B + m∠C  =  180°

Substitute 59° for m∠B and 55° for m∠C.  

m∠A + 59° + 55°  =  180°

Simplify. 

m∠A + 114°  =  180°

Subtract 114° from both sides. 

m∠A  =  66°

By the Third Angles Theorem, if two angles of one triangle are congruent to two angles of another triangle, then the third angles are also congruent.

So, we have 

∠T ≅ ∠A

m∠T = ∠A

m∠T =  66°

3. Answer : 

In the diagram above, ∠N ≅ ∠R and ∠L ≅ ∠S. From the Third angles theorem, we know that ∠M ≅ ∠T. So, m∠M = m∠T.

From the triangle sum theorem, we have 

m∠L + m∠M + m∠N  =  180°

65° + 55° + m∠M  =  180°

Simplify

120° + m∠M  =  180°

Subtract 120° from both sides. 

m∠M  =  60° 

By the theorem, if two angles of one triangle are congruent to two angles of another triangle, then the third angles are also congruent.

So, we have

∠M ≅ ∠T ----> m∠M = m∠T

Substitute 60° for m∠M and (2x + 30)° for m∠M.

60°  =  (2x + 30)°

60  =  2x + 30

Subtract 30 from both sides.

30  =  2x

Divide both sides by 2. 

15  =  x

4. Answer : 

In the diagram above, we are given that all three pairs of corresponding sides are congruent. 

RP ≅ MN, PQ ≅ NQ and QR ≅ QM

Because ∠P and ∠N have the same measure, ∠P ≅ ∠N.

By the Vertical Angles Theorem, we know that 

∠PQR ≅ ∠MQN

In ΔPQR and ΔMQN, ∠P ≅ ∠N and ∠PQR ≅ ∠MQN.  

By the theorem, if two angles of one triangle are congruent to two angles of another triangle, then the third angles are also congruent.

So, we have

∠R ≅ ∠M

So, all three pairs of corresponding sides and all three pairs of corresponding angles are congruent.

By the definition of congruent angles, 

ΔPQR ≅ ΔNQM

5. Answer : 

The figure shows that the two triangles share a vertical pair of angles, so they have one congruent angle in common, but the markings also show that there are no other congruent corresponding angles.

Answer: The two triangles are not similar.

6. Answer : 

The figure shows that the two triangles have two pairs of congruent corresponding angles Thus, they are similar according to the AA Triangle Similarity Postulate.

Corresponding angles are ∠𝑈 𝑎𝑛𝑑 ∠𝐿, ∠𝑇 𝑎𝑛𝑑 ∠𝐾, ∠𝑉 𝑎𝑛𝑑 ∠𝐽.

Answer: Reason: AA, ∆𝑈𝑇𝑉 ~ ∆𝐿𝐾J

7. Answer : 

The figure shows that the two triangles share a vertical pair of angles, so they have one congruent angle in common, and the markings also show that there is one other pair of congruent corresponding angles.

Corresponding angles are ∠𝑈 and ∠𝐶,∠𝑇 and ∠𝐵, ∠𝑇𝑆𝑈 and ∠𝐵𝑆𝐶.

Answer: Reason: AA, ∆𝑈𝑇𝑆~∆𝐶𝐵S

8. Answer : 

The figure shows that the two triangles share a vertical pair of angles, so they have one congruent angle in common, and the figure also show that there is a 61° angle in each triangle.

Therefore, the triangles are similar by the AA Triangle Similarity Postulate. Corresponding angles are ∠𝐻 and ∠𝐺, ∠𝐻𝑆𝑇 and ∠𝐺𝑆𝐹,∠𝑇 and ∠𝐹.

Answer: Reason: AA, ∆𝐻𝑆𝑇~∆𝐺𝑆E

9. Answer : 

Vertically opposite angles are equal.

<VRU = <SRT = 95

<RVU + <VRU + <RUV = 180

37 + 95 + <RUV = 180

132 + <RUV = 180

<RUV = 180 - 132

<RUV = 48

<RST = 48

Since the triangles are equiangular, then the triangles are similar.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.