TOTAL SURFACE AREA
Key Concept
Consider the cuboid shown below.
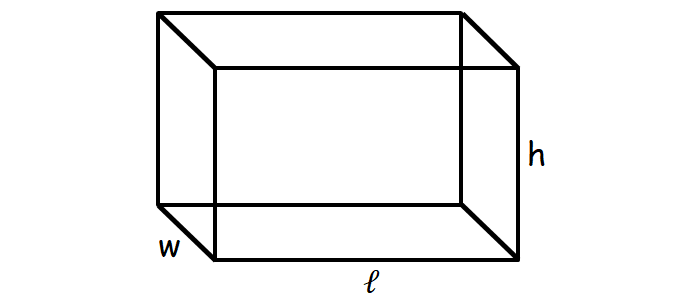
To find the lateral surface area of the cuboid, we will add the areas of the four side walls.
Lateral Surface Area of a Cuboid :
= 2ℓh + 2hw square units
To get the total surface area of a cuboid, we have to include the area of the bases, which are top and bottom.
Total Surface Area of a Cuboid :
= 2ℓh + 2hw + 2ℓw
= 2(ℓh + hw + ℓw) square units
Total surface area of a 3D figure refers to the area which cover the bases and and the curved part or side walls. In other words, the total surface area is the area which cover the areas of all faces of an object.
Total Surface Area of a Cube
The sum of the areas of all the six equal faces is called the total Surface Area of the cube. In the figure shown below, let the side of the cube measure a units.
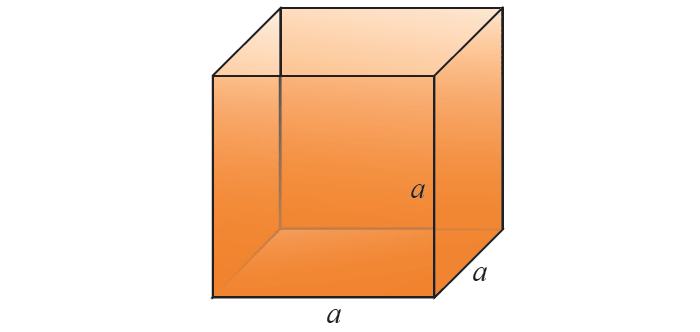
Then the area of each face of the cube is a2 square units.
Hence, the total surface area is 6a2 square units.
In a cube, if we don’t consider the top and bottom faces, the remaining area is called the lateral surface area. Hence, the lateral surface area of the cube is 4a2 square units.
Total Surface Area of a Cylinder
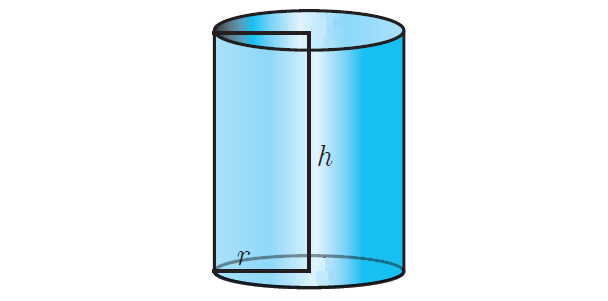
Total surface area of a cylinder refers to the sum of areas of the curved surface and the two circular regions at the top and bottom.
That is, total surface area of a right circular cylinder :
= curved surface area + areas of the top region + area of the bottom region
= 2πrh + πr2 + πr2
= 2πrh + 2πr2
= 2πr(h + r) square units
Total Surface Area of a Cone
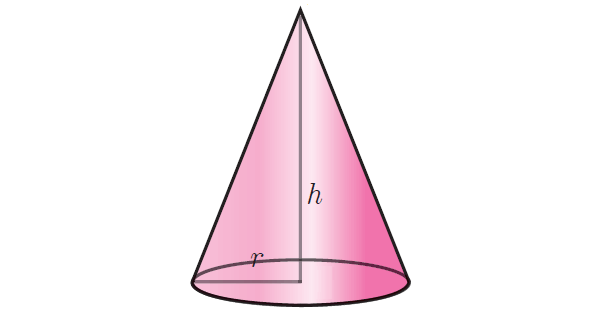
Total surface area of a cone refers to the sum of areas of the curved surface and the circular region at the bottom.
That is, total surface area of a right circular cone :
= curved surface area + area of the bottom region
= πrℓ + πr2
= πr(ℓ + r) square units
Total Surface Area of a Sphere
Place a sphere inside a right circular cylinder of equal diameter and height.
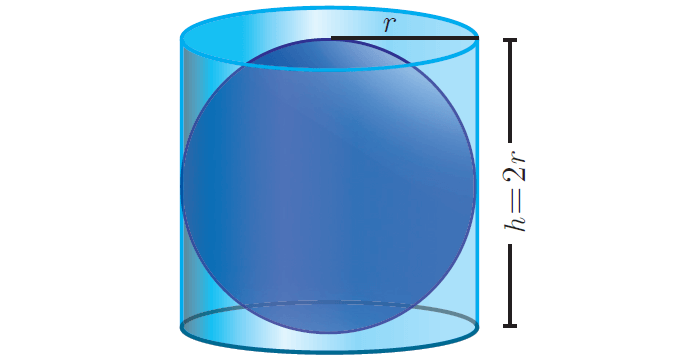
Then the height of the cylinder will be the diameter of the sphere. In this case, Archimedes proved that the outer area of the sphere is same as curved surface area of the cylinder.
That is, total surface area of sphere :
= curved surface area of cylinder
= 2πrh
= 2πr(2r)
= 4πr2 square units
Total Surface Area of a Hemisphere
A section of the sphere cut by a plane through any of its great circle is a hemisphere.
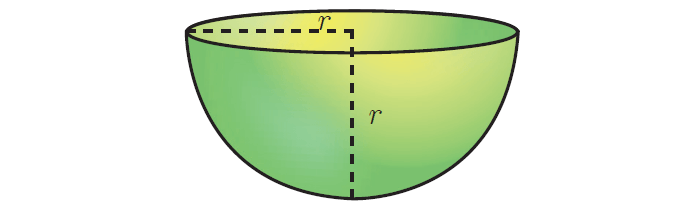
By doing this, we observe that a hemisphere is exactly half the portion of the sphere.
Curved surface area of hemisphere :
= ½ ⋅ curved surface area of sphere
= ½ ⋅ 4πr2
= 2πr2 square units
Total surface area of hemisphere :
= curved surface area + area of top circular region
= 2πr2 + πr2
= 3πr2 square units
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Multi Step Algebra Word Problems
Apr 23, 24 09:10 PM
Multi Step Algebra Word Problems -
Solving Multi Step Word Problems Worksheet
Apr 23, 24 12:32 PM
Solving Multi Step Word Problems Worksheet -
Solving Multi Step Word Problems
Apr 23, 24 12:07 PM
Solving Multi Step Word Problems
