TRANSFORMATIONS AND SIMILARITY WORKSHEET 

Problem 1 :

A rectangle has the vertices (-6, 8), (-2, 8), (-2, 6) and (-6, 6).  Apply the indicated series of transformations to the triangle. Each transformation is applied to the image of the previous transformation, not the original figure. Label each image with the steps of the transformation applied.

(i)  (x, y) → (x + 7, y - 2)

(ii)  Reflection across the x-axis.

(iii)  Clockwise rotation of 90° around the origin

(iv)  (x, y) → (x + 5, y + 3)

(v)  Dilation about the origin with scale factor 3.

Compare the size and shape of the final image to that of the original figure.

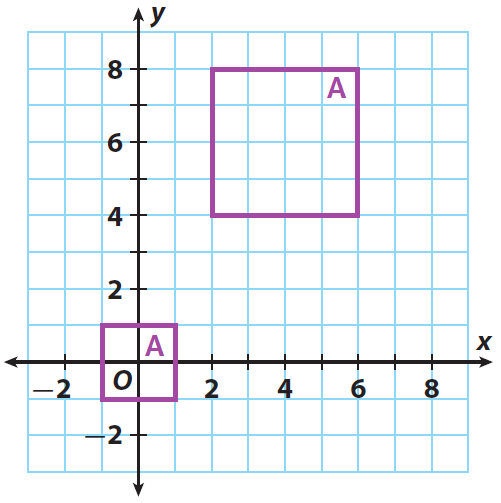
Problem 2 :

Identify a sequence of transformations that can transform figure A into figure B. Say whether the figures are congruent. And also, say whether they are similar.

Problem 3 :

Identify a sequence of transformations that can transform figure X into figure Y. Include a reflection. Say whether the figures are congruent. And also, say whether they are similar.

Problem 1 :

A rectangle has the vertices (-6, 8), (-2, 8), (-2, 6) and (-6, 6).  Apply the indicated series of transformations to the triangle. Each transformation is applied to the image of the previous transformation, not the original figure. Label each image with the steps of the transformation applied.

(i)  (x, y) → (x + 7, y - 2)

(ii)  Reflection across the x-axis.

(iii)  Clockwise rotation of 90° around the origin

(iv)  (x, y) → (x + 5, y + 3)

(v)  Dilation about the origin with scale factor 3.

Compare the size and shape of the final image to that of the original figure.

Solution :

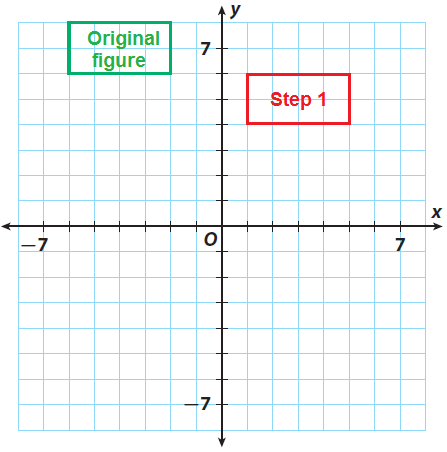
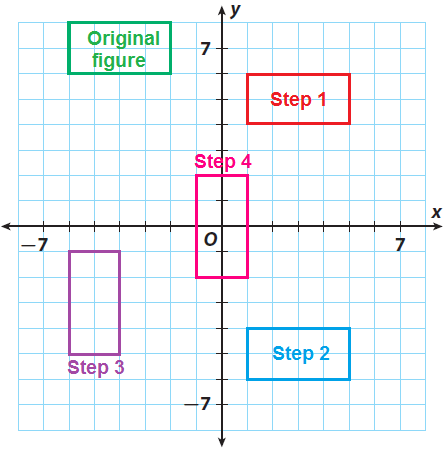
Step 1 : 

(i)   (x, y) → (x + 7, y - 2).

(-6, 8) -----> (1, 6) 

(-2, 8) -----> (5, 6)

(-2, 6) -----> (5, 4)

(-6, 6) -----> (1, 4) 

Graph the image.

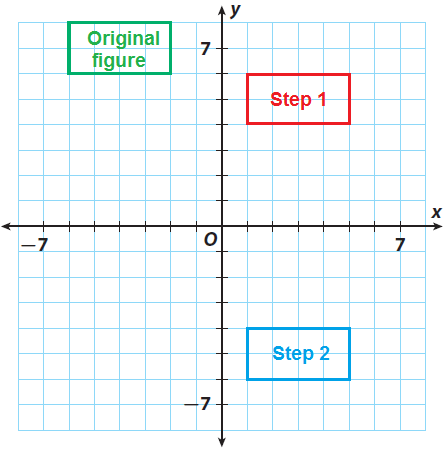
Step 2 : 

(ii)  Reflection across the x-axis.

Since there is a reflection across the x-axis, we have to multiply each y-coordinate by -1. That is,

(x, y) -----> (x, -y) 

So, we have 

(1, 6) -----> (1, -6) 

(5, 6) -----> (5, -6)

(5, 4) -----> (5, -4)

(1, 4) -----> (1, -4) 

Graph the image.

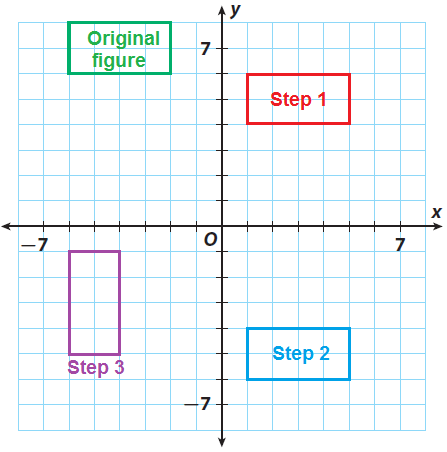
Step 3 : 

(iii)  Clockwise rotation of 90° around the origin.

Since there is a rotation of 90° clockwise about the origin, we have multiply each x-coordinate by -1 and interchange x and y coordinates. That is,

(x, y) -----> (y, -x) 

So, we have 

(1, -6) -----> (-6, -1)

(5, -6) -----> (-6, -5)

(5, -4) -----> (-4, -5)

(1, -4) -----> (-4, -1) 

Graph the image.

Step 4 : 

(iii)  (x, y) → (x + 5, y + 3)

(-6, -1) -----> (-1, 2)

(-6, -5) -----> (-1, -2)

(-4, -5) -----> (1, -2)

(-4, -1) -----> (1, 2) 

Graph the image.

Step 5 : 

(iii)  (x, y) → (3x, 3y)

(-1, 2) -----> (-3, 6)

(-1, -2) -----> (-3, -6)

(1, -2) -----> (3, -6)

(1, 2) -----> (3, 6) 

Graph the image.

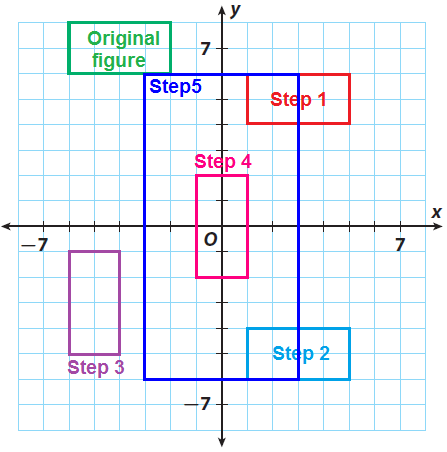
Compare the size and shape of the final image to that of the original figure.

Shape :

Same shape

Size : 

The sides of rectangle E are three times the lengths of the sides of the original figure.

Angle Measures : 

Same angle measures

Problem 2 :

Identify a sequence of transformations that can transform figure A into figure B. Say whether the figures are congruent. And also, say whether they are similar.

Solution : 

Step 1 : 

Both figures are squares whose orientations are the same, so no reflection or rotation is needed.

Step 2 : 

Figure B has sides twice as long as figure A, so a dilation with a scale factor of 2 is needed.

Step 3 :

Figure B is moved to the right and above figure A, so a translation is needed.

Step 4 : 

A sequence of transformations that will accomplish this is a dilation by a scale factor of 2 centered at the origin followed by the translation

(x, y) ----> (x + 4, y + 6)

The figures are not congruent, but they are similar.

Problem 3 :

Identify a sequence of transformations that can transform figure X into figure Y. Include a reflection. Say whether the figures are congruent. And also, say whether they are similar.

Solution : 

Step 1 : 

The orientation of figure Y is reversed from that of figure X, so a reflection over the y-axis is needed.

Step 2 : 

Figure Y has sides that are half as long as figure X, so a dilation with a scale factor of 1/2 is needed.

Step 3 :

Figure B is moved to the right and above figure A, so a translation is needed.

Step 4 : 

Figure Y is moved above figure X, so a translation is needed.

Step 5 : 

A sequence of transformations that can accomplish this is a dilation by a scale factor of 1/2 centered at the origin, followed by the reflection

(x, y) ---> (-x , y)

followed by the translation

(x, y) ---> (x , y + 5)

The figures are not congruent, but they are similar.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.