TRANSFORMATIONS ON THE COORDINATE PLANE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
We can perform transformations on a coordinate plane by changing the coordinates of the points on a figure. The points on the translated figure are indicated by the prime "symbol" to distinguish them from the original points
|
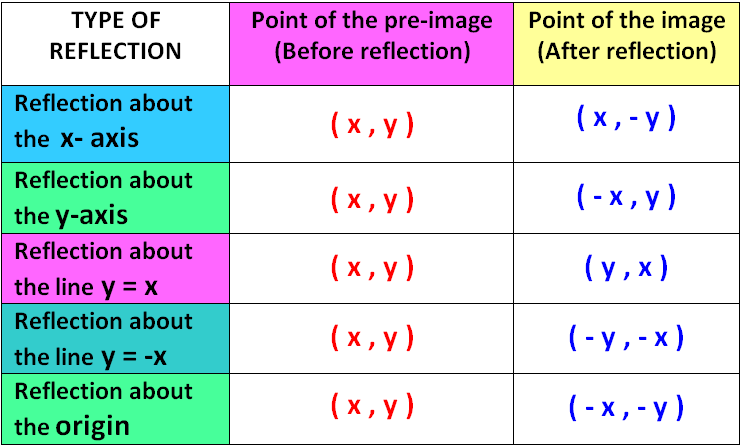
A point on a coordinate plane can be reflected across an axis. The reflection is located on the opposite side of the axis, at the same distance from the axis. | |
|
A translation "slides" an object a fixed distance in a given direction. The original object and its translation have the same shape and size, and they face in the same direction. It is a direct isometry. | |
|
A dilation is a transformation that produces an image that is the same shape as the original, but is a different size. NOT an isometry. Forms similar figures. | |
|
To rotate a figure 90 degree clockwise about the origin, switch the coordinates of each point and then multiply the new first coordinate by -1. To rotate 180 degree about origin, multiply both coordinates of each point by -1. |
Reflection on Coordinate Plane
Examples
Example 1 :
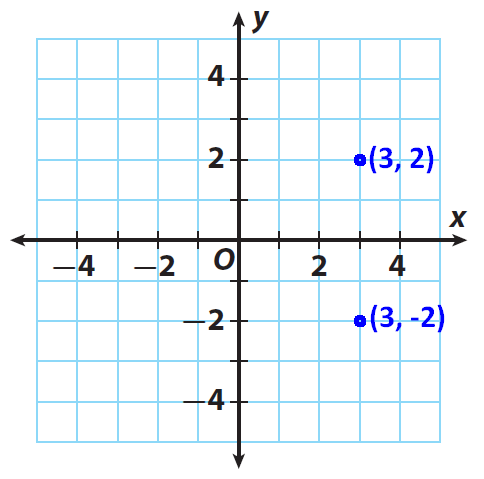
Graph (3, −2). Then fold your coordinate plane along the y-axis and find the reflection of (3, −2). Record the coordinates of the new point in the table.
Solution :
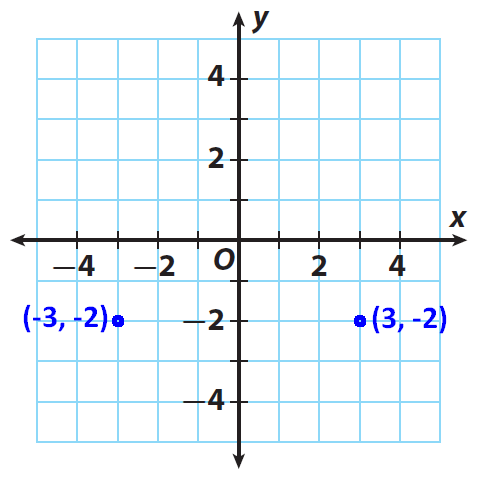
Example 2 :
Graph (3, −2). Then fold your coordinate plane along the x-axis and find the reflection of (3, −2). Record the coordinates of the new point in the table.
Solution :
Reflection about the x-axis

Reflection about the y-axis

Reflection about the line y=x

Once students understand the rules which they have to apply for reflection transformation, they can easily make reflection -transformation of a figure.
For example, if we are going to make reflection transformation of the point (2,3) about x-axis, after transformation, the point would be (2,-3). Here the rule we have applied is (x, y) ------> (x, -y).
So we get (2,3) -------> (2,-3).
Translation on Coordinate Plane
Translation of (h, k) :
(x, y) -----> (x + h, y + k)
Example 3 :
Let A ( -2, 1), B (2, 4) and (4, 2) be the three vertices of a triangle. If this triangle is translated for ( h, k ) = ( 2, 3) what will be the new vertices A' , B' and C' ?
Solution :
Step 1 :
First we have to know the correct rule that we have to apply in this problem.
Step 2 :
Here triangle is translated for (h , k ) = ( 2 , 3 ).
So the rule that we have to apply here is
(x, y) -------> (x + h, y + k)
Step 3 :
Based on the rule given in step 1, we have to find the vertices of the translated triangle A'B'C'
Step 4 :
(x , y) -----> (x + h, y + k)
A(-2, 1) -------> A'(0, 4)
B(2, 4) -------> B'(4, 7)
C(4, 2) -------> C'(6, 5)
Step 5 :
Vertices of the translated triangle are
A'(0, 4), B(4, 7) and C'(6, 5)
Dilation on the Coordinate Plane
Dilation of scale factor "k" :
(x, y) -----> (kx, ky)
Dilation for "k = 2".
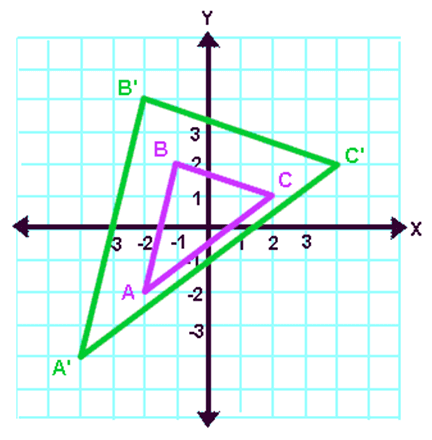
Example 4 :
Let A(-2, -2), B(-1, 2) and C(2, 1) be the three vertices of a triangle. If this triangle is dilated for the scale factor "k = 2", what will be the new vertices A', B' and C' ?
Solution:
Step 1 :
First we have to know the correct rule that we have to apply in this problem.
Step 2 :
Here, triangle is dilated for the scale factor "k = 2".
So, the rule that we have to apply here is
(x, y) -------> (kx , ky)
Step 3 :
Based on the rule given in step 1, we have to find the vertices of the dilated triangle A'B'C'
Step 4 :
(x, y) -----> (kx, ky)
A(-2, -2) -------> A'(-4, -4)
B(-1, 2) -------> B'(-2, 4)
C(2, 1) -------> C'(4, 2)
Step 5 :
Vertices of the dilated triangle are
A'(-4, -4), B(-2, 4) and C'(4, 2)
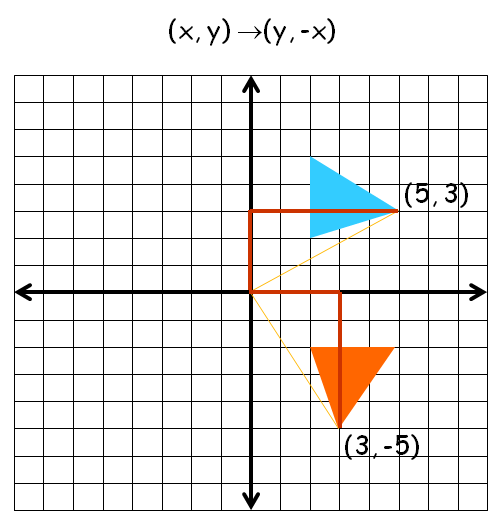
Rules on Finding Rotated Image

90° Rotation (clock wise)
90° Rotation (counter clock wise)

180° Rotation (clock wise and counter clock wise)
Example 5 :
Let A(-2, 1), B(2, 4) and C(4, 2) be the three vertices of a triangle. If this triangle is rotated about 90° clockwise, what will be the new vertices A', B' and C' ?
Solution :
Step 1 :
First we have to know the correct rule that we have to apply in this problem.
Step 2 :
Here triangle is rotated about 90° clock wise. So the rule that we have to apply here is
(x, y) -------> (y, -x)
Step 3 :
Based on the rule given in step 1, we have to find the vertices of the reflected triangle A'B'C'.
Step 4 :
(x, y) -----> (y, -x)
A(-2, 1) -------> A'(1, 2)
B(2, 4) -------> B'(4, -2)
C(4, 2) -------> C'(2, -4)
Step 5 :
Vertices of the reflected triangle are
A'(1, 2), B(4, -2) and C'(2, -4)
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact US | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
10 Hard SAT Math Questions (Part - 39)
Dec 11, 25 05:59 PM
10 Hard SAT Math Questions (Part - 39) -
10 Hard SAT Math Questions (Part - 38)
Dec 08, 25 12:12 AM
10 Hard SAT Math Questions (Part - 38) -
SAT Math Practice
Dec 05, 25 04:04 AM
SAT Math Practice - Different Topics - Concept - Formulas - Example problems with step by step explanation

