TRANSFORMING ABSOLUTE VALUE FUNCTIONS WORKSHEET

Problem 1 :

Describe the transformations from the graph of f(x) = |x| to the graph of g(x). Then graph both functions.

g(x)  =  -|x|

Problem 2 : 

Describe the transformations from the graph of f(x) = |x| to the graphs of g(x) and h(x). Then graph all the three functions.

g(x)  =  3|x|

h(x)  =  (1/2)|x|

Problem 3 : 

Describe the transformations from the graph of f(x) = |x| to the graphs of g(x) and h(x). Then graph all the three functions.

g(x)  =  |x + 2|

h(x)  =  |x - 2|

Problem 4 : 

Describe the transformations from the graph of f(x) = |x| to the graphs of g(x) and h(x). Then graph all the three functions.

g(x)  =  |x| + 2

h(x)  =  |x| - 2

Problem 5 :

Describe the transformations from the graph of f(x) = |x| to the graph of g(x). Then graph both functions.

g(x)  =  2|x + 1|

Problem 6 : 

g (x)  =  -|x - 3| + 2

Problem 7 :

In a charity race, a water stand for the runners is halfway between the start and finish lines. The absolute value function y = |(x/8) - 3|models Riley’s distance y in miles from the water stand x minutes into the race. The function y = |(x/10) - 3| models Dean’s distance from the water stand during the same race. Compare Dean’s graph to Riley’s graph. What can you conclude about Dean’s speed?

Answers

1. Answer :

Identify a, b, and c.

g(x) = -|x|.

• a = -1 : graph opens downward and width is unchanged

• b = 0 : no horizontal translation

• c = 0 : no vertical translation

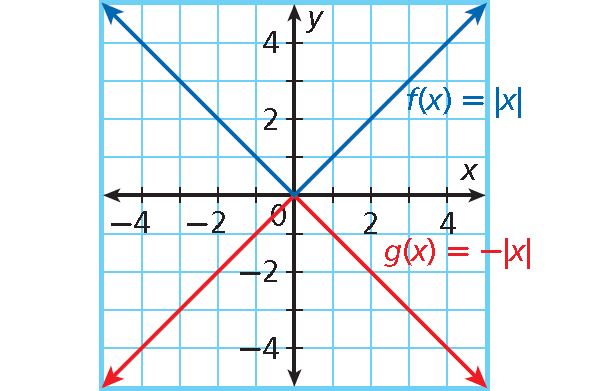
2. Answer :

Identify a, b, and c.

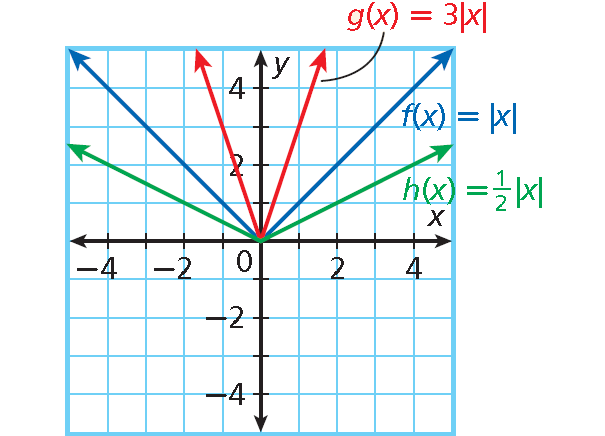
3. Answer :

Identify a, b, and c.

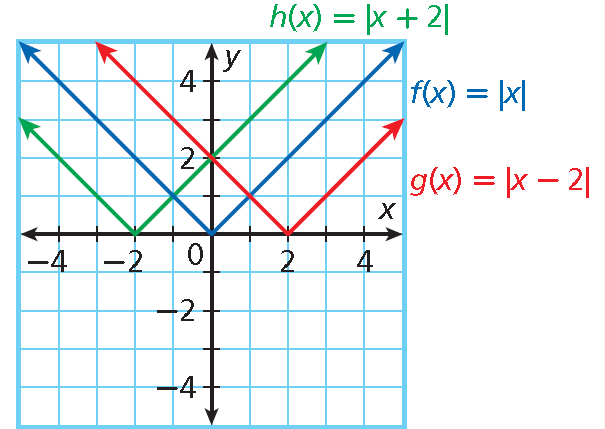
4. Answer :

Identify a, b, and c.

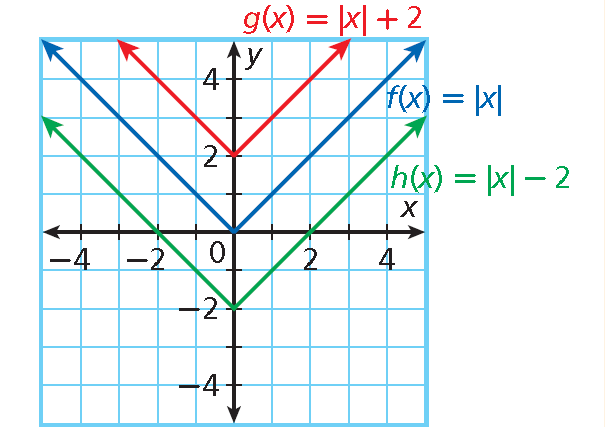
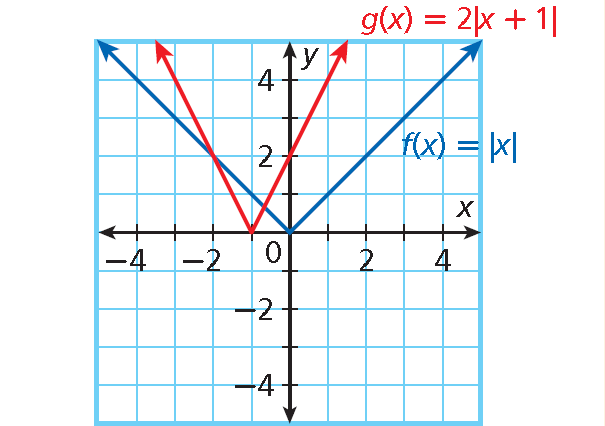
5. Answer :

Identify a, b, and c.

g(x) = 2|x + 1| = 2|x – (–1)| + 0.

• a = 2 : graph is narrower

• b = –1 : translated 1 unit left

• c = 0 : no vertical translation

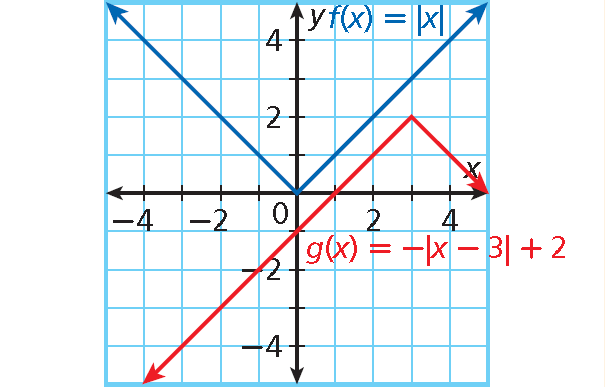
6. Answer :

Identify a, b, and c.

g(x) = -|x - 3| + 2 = -1|x – 3| + 2.

• a = -1 : graph opens downward and width is unchanged

• b = 3 : translated 3 units right

• c = 2 : translated 2 units up

7. Answer :

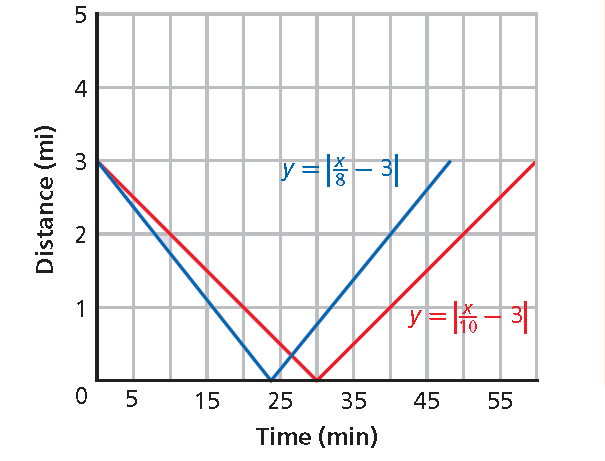
y = |(x/8) - 3| is graphed in blue. 

y = |(x/10) - 3| is graphed in red. Both graphs start at the same point, but Dean’s graph is translated to the right. It takes him more time to reach the water stand and to finish the race. Therefore, he is running more slowly than Riley.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.