TRANSFORMING LINEAR FUNCTIONS WORKSHEET

Problem 1 : 

Graph f(x) = x and g(x) = x - 5. Then describe the transformation from the graph of f(x) to the graph of g(x).

Problem 2 : 

Graph f(x) = x + 2 and g(x) = 2x + 2. Then describe the transformation from the graph of f(x) to the graph of g (x) .

Problem 3 : 

f(x)  =  x

Problem 4 : 

f(x)  =  -4x - 1

Problem 5 : 

Graph f(x) = x and g(x) = 3x + 1. Then describe the transformations from the graph of f(x) to the graph of g(x).

Problem 6 : 

A trophy company charges $175 for a trophy plus $0.20 per letter for the engraving. The total charge for a trophy with x letters is given by the function f(x) = 0.20x + 175. How will the graph change if the trophy’s cost is lowered to $172? if the charge per letter is raised to $0.50?

Problem 7 : 

Graph f(x) = x and g(x) = −2x + 3. Describe the transformations from the graph of f to the graph of g.

Problem 8 : 

A cable company charges customers $60 per month for its service, with no installation fee. The cost to a customer is represented by c(m) = 60m, where m is the number of months of service. To attract new customers, the cable company reduces the monthly fee to $30 but adds an installation fee of $45. The cost to a new customer is represented by r(m) = 30m + 45, where m is the number of months of service. Describe the transformations from the graph of c to the graph of r.

Use the graphs of f and g to describe the transformation from the graph of f to the graph of g.

Problem 9 :

Problem 10 :

Detailed Answer Key

1. Answer : 

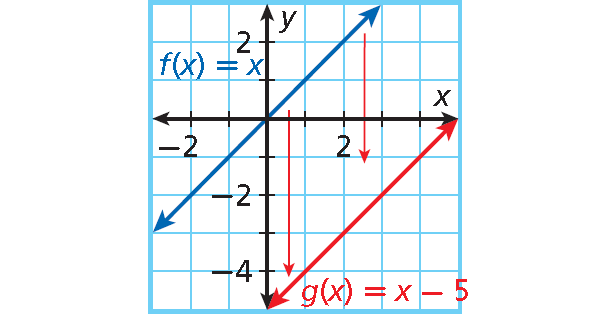
The graph of g(x) = x - 5 is the result of translating the graph of f(x) = x, 5 units down.

2. Answer : 

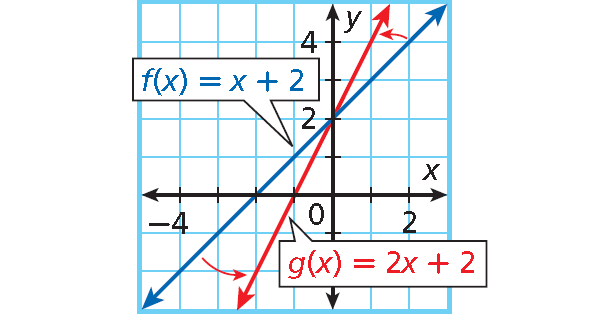
The graph of g(x) = 2x + 2 is the result of rotating the graph of f(x) = x + 2 about (0, 2). The graph of g(x) is steeper than the graph of f(x).

3. Answer : 

To find g(x), multiply the value of m by -1.

In f(x) = x, m = 1.

1(-1)  =  -1   This is the value of m for g(x).

g(x) = -x

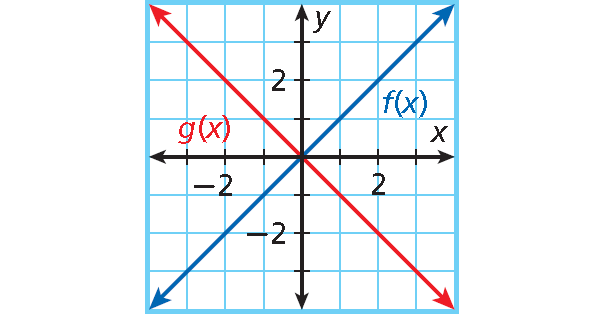
4. Answer : 

To find g(x), multiply the value of m by -1.

In f(x) = -4x - 1, m = -4.

-4(-1)  =  4   This is the value of m for g(x).

g(x) = 4x - 1 

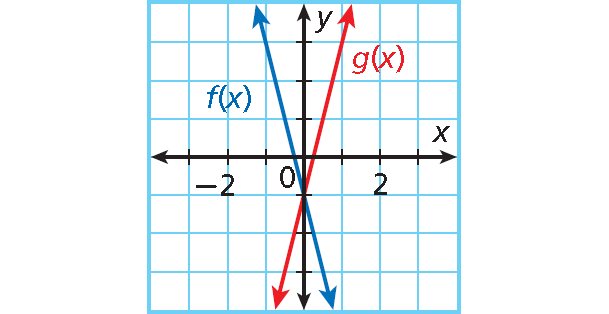
5. Answer : 

• Find transformations of f(x) = x that will result in g(x) = 3x + 1 :
• Multiply f(x) by 3 to get h(x) = 3x. This rotates the graph about (0, 0) and makes it steeper.
• Then add 1 to h(x) to get g(x) = 3x + 1. This translates the graph 1 unit up.

The transformations are a rotation and a translation.

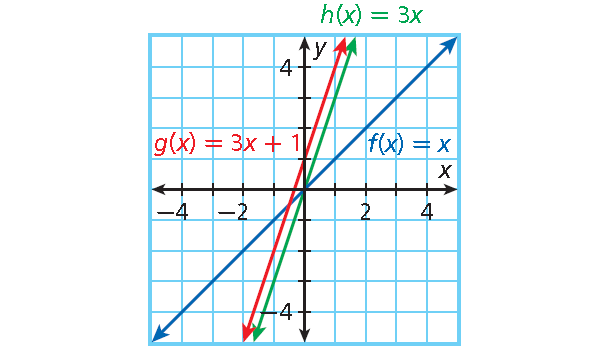
6. Answer : 

f(x) = 0.20x + 175 is graphed in blue.

If the trophy’s cost is lowered to $172, the new function is g(x) = 0.20x + 172. The original graph will be translated 3 units down. 

If the charge per letter is raised to $0.50, the new function is h(x) = 0.50x + 175. The original graph will be rotated about (0, 175) and become steeper.

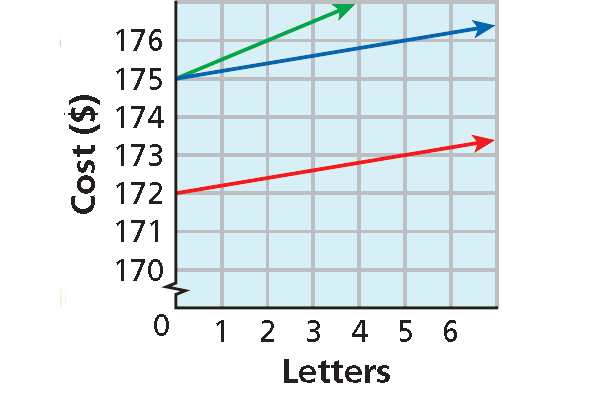
7. Answer :

Given that f(x) = x

Note that you can rewrite g as g(x) = −2f(x) + 3.

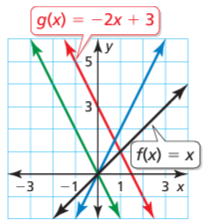
Step 1 :

There is no horizontal translation from the graph of f to the graph of g.

Step 2 :

Stretch the graph of f vertically by a factor of 2 to get the graph of h(x) = 2x.

Step 3 :

Reflect the graph of h in the x-axis to get the graph of r(x) = −2x.

Step 4 :

Translate the graph of r vertically 3 units up to get the graph of g(x) = −2x + 3.

8. Answer :

Note that you can rewrite r as r(m) = (1/2) c(m) + 45. In this form, you can use the order of operations to get the outputs of r from the outputs of c.

First, multiply the outputs of c by 1/2 to get h(m) = 30m.

Then add 45 to the outputs of h to get r(m) = 30m + 45.

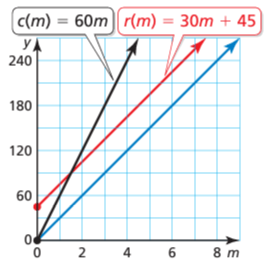
The transformations are a vertical shrink by a factor of (1/2)   and then a vertical translation 45 units up.

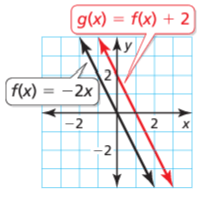
9 Answer :

Given that f(x) = -2x

g(x) = f(x) + 2

g(x) = -2x + 2

g(x) = f(x) + 2

g(x) = -2x + 2

The graph is moved towards up 2 units.

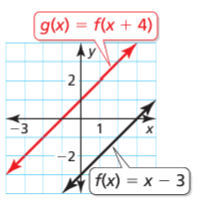
10  Answer :

Given that f(x) = x - 3

g(x) = f(x + 4)

g(x) = x + 4 - 3

= x + 1

Moving the graph towards left of 4 units.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.