TRANSLATING VERBAL PHRASES TO ALGEBRAIC EXPRESSIONS

Example 1  :

Two numbers have a sum of 4. If one of them is s then the other is ?

Solution :

Sum of two numbers  =  4

One number + other number  =  4

s + other number  =  4

other number  =  4 – s

So, the required other number is 4 - s.

Example 2 :

The sum of two numbers is 13. One of the numbers is x. what is the Other number ?

Solution :

Sum of two numbers  =  13

One number + other number  =  13

x + other number  =  13

other number  =  13 – x

Example 3 :

Two numbers are in the ratio 1 : 2 . If the smaller one is a then the larger One is ?

Solution :

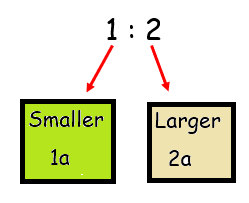
So, the larger part is 2a.

Example 4 :

Two numbers in the ratio 2 : 3 can be represented by 2c and … ?

Solution :

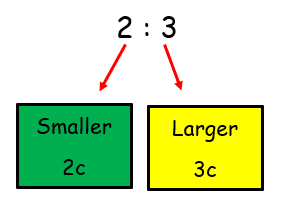
Example 5 :

If there are 27 students in a class and "b" are boys, then there are … girls ?

Solution :

Total number of students  =  27

number of boys + number of girls  =  27 students

b + girls  =  27

girls  =  27 – b

Example 6 :

There are "s" students in a class. If "g" of them are girls, how many of them  are boys ?

Solution :

number of boys + number of girls  =  s students

boys + g  =  s

boys  =  s – g

Example 7 :

If the smaller of two consecutive integers is y, then the larger is… ?

Solution :

Given, Smaller integer is y

Larger integer is y + 1

Example 8 :

The larger of two consecutive integers is k. what is the smaller integer?

Solution :

For example, 

If "x" be the first integer, then x+1, x+2,....... are consecutive integers.

x < (x+1) and (x+1) < (x+2)

Then smaller of x is (x-1).

Given, larger integer is k

smaller integer is k – 1

Example 9 :

The larger of two consecutive odd integers is v. what is the smaller one?

Solution :

Given, larger odd integer is v

Smaller one is v – 2

Example 10 :

n is the smallest of three consecutive integers. What are the other two integers ?

Solution :

Given, smallest integer is n

If n is the first number, then

n+1, n+2, ................

are consecutive numbers.

So, the other two numbers are n+1 and n+2.

Example 11 :

Three consecutive integers in ascending order are

x, …, … ?

Solution :

Given, first integer is x

Second number  =  x + 1

Third number  =  x + 2

So, three consecutive integers in ascending order are x, x + 1, x + 2.

Example 12 :

Three consecutive integers in descending order are

a, …, … ?

Solution :

Given, first integer is a

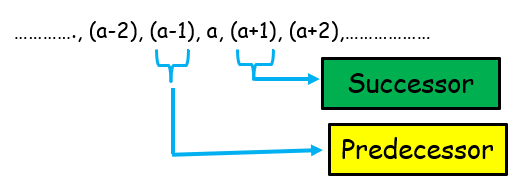
So, Three consecutive integers in descending order are a, a - 1, a – 2.

Example 13 :

If the middle integer of three consecutive integers is m, then the other two are …… ?

Solution :

Given, middle integer is m

Predecessor  =   m - 1

Successor  =  m + 1

So, other two are m – 1 and m + 1

Example 14 :

The middle integer of three consecutive even integers is m. what are the other two integers ?

Solution :

Given, middle even integer is m

Predecessor  =  m - 2

Successor  =  m + 2

So, other two are m – 2 and m + 2

Example 15 :

Two numbers differ by 3. If the smaller one is s then the other is ?

Solution :

Larger number - Smaller number  =  3

Other number  =  Large number

Large number - s  =  3

Large number  =  3+s

So, the other number is 3+s.

Example 16 :

Two consecutive odd integers in ascending order are d and … ?

Solution :

Given, one odd integer is d

Predecessor  =  d+2

Example 17 :

Shiv works in a mall and gets paid $50 per hour. Last week he worked for 7 hours and this week he will work for x hours. Write an algebraic expression for the money paid to him for both the weeks.

Solution :

Amount earned per hour = $50

Number of hours he worked last week = 7

Number of hours he worked = x

Total number of hours he worked sofar = 7 + x

Amount paid = 50(7 + x)

Using distributive property, we get

= 350 + 50x

Example 18 :

Sonu and Raj have to collect different kinds of leaves for science project. They go to a park where Sonu collects 12 leaves and Raj collects x leaves. After some time Sonu loses 3 leaves and Raj collects 2x leaves. Write an algebraic expression to find the total number of leaves collected by both of them.

Solution :

Number of leaves collected by Sonu = 12

Number of leave Raj collects = x

After some time,

Number of leaves Sonu has = 12 - 3 ==> 9

Number of leaves Raj has = 2x

Total number of leaves collected = 9 + 2x

Example 19 :

A school has a rectangular play ground with length x and breadth y and a square lawn with side x as shown in the figure given below. What is the total perimeter of both of them combined together?

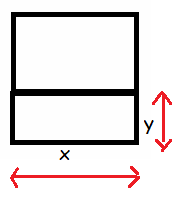
Solution :

Perimeter of the shape = sum of lengths of all sides

= x + y + y + x + x + x

= 4x + 2y

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.