TRANSLATION OF THE IMAGE UNDER THE POINT PRACTICE PROBLEMS

Problem 1 :

Find the image equation when 3x + 2y = 8 is translated under the vector <-1, 3>.

Solution :

Let us find any two points on the straight line 3x + 2y = 8

Converting 3x + 2y = 8 to intercept form, we get

(3x/8)+(2y/8)  =  8/8

x/(8/3) + y/4  =  1

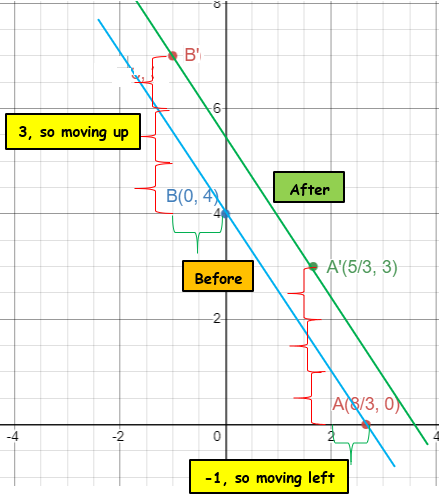
Point on x-intercept is A(8/3, 0).

Point on y-intercept is B(0, 4).

Here (h, k)  ==>  (-1, 3)

x'  =  x-1 and y'  =  y+3

Problem 2 :

Find the image equation when 2x - y = 6 is translated under the vector <-3, 0>.

Solution :

Let us find any two points on the straight line 2x - y = 6

Converting 2x - y = 6 to intercept form, we get

(2x/6) - (y/6) = 6/6

x/3 - y/6  =  1

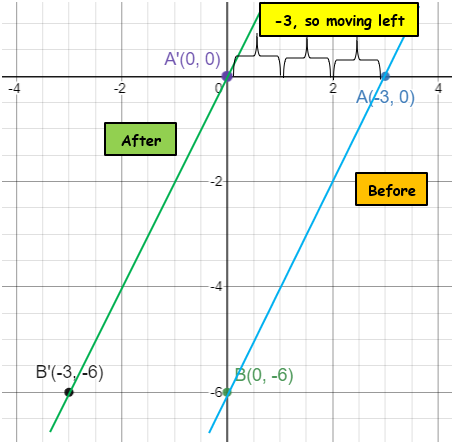
Point on x-intercept is A(3, 0).

Point on y-intercept is B(0, -6).

Here (h, k)  ==>  (-3, 0)

x'  =  x-3 and y'  =  y+0

Problem 3 :

Find the image equation when y  =  x² is translated under the vector <0, 3>.

Solution :

Let us find any three points on the parabola y  =  x²

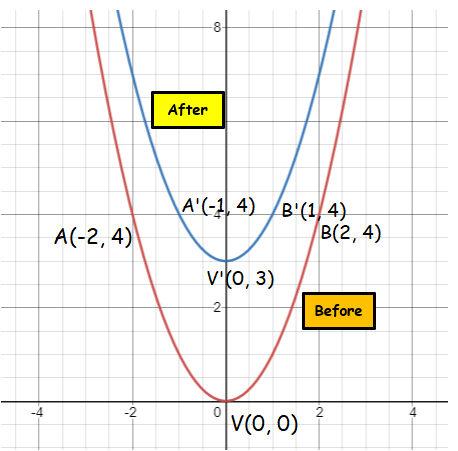
Finding vertex  ==>  V(0, 0)

If x  =  -2, then y  =  4  ==>  A(-2, 4)

If x  =  2, then y  =  4  ==>  B(2, 4)

Here (h, k)  ==>  (0, 3)

Problem 4 :

Find the image equation when xy  =  -8 is translated under the vector <3, -2>.

Solution :

Let us find any three points on the rectangular parabola xy  =  -8

Finding 4 point on the rectangular hyperbola,

y  =  -8/x

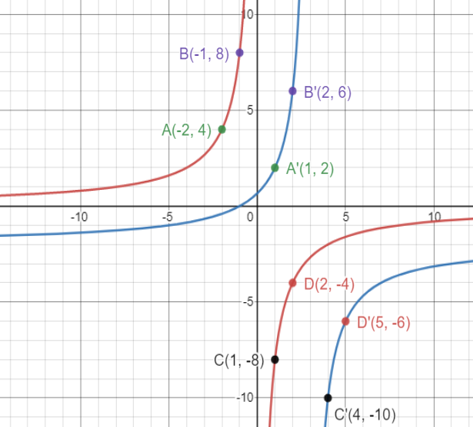
If x = -2, then y = 4  ==>  A(-2, 4)

If x = -1, then y = 8  ==>  B(-1, 8)

If x = 1, then y = -8  ==>  C(1, -8)

If x = 2, then y = -4  ==>  D(2, -4)

Here (h, k)  ==>  (3, -2)

x'  =  x+3 and y'  =  y-2

x coordinate is +3, so we have to move old x coordinate 3 units right.

y coordinate is -2, so we have to move old y coordinate 2 units down.

Problem 5 :

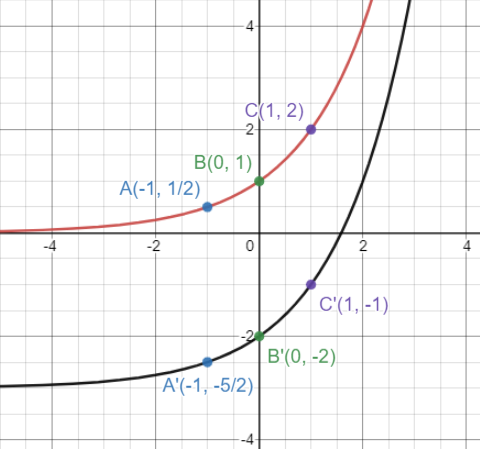
Find the image equation when y  =  2^x is translated under the vector <0, -3>.

Solution :

Finding 3 points on the exponential function.

y  =  2^x

If x = -1, then y = 1/2  ==>  A(-1, 1/2)

If x = 0, then y = 1  ==>  B(0, 1)

If x = 1, then y = 2  ==>  C(1, 2)

Here (h, k)  ==>  (0, -3)

x'  =  x+0 and y'  =  y-3

No need of horizontal movements, but move the y-coordinate 3 units down.

Problem 6 :

A trapezoid is translated 7 units to the right and then reflected across the x-axis.

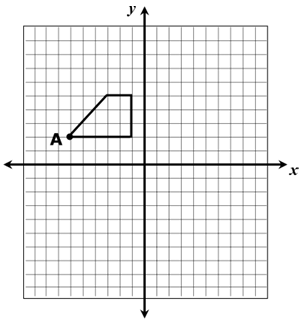
Which ordered pair describes the image of point A ?

a)  (1, 2)    b) (1, -2)    c)  (-1, 2)     d)  (-6, -5)

Solution :

The point A is (-6, 2). This point is translated 7 units right.

A(-6, 2) ==> A'(-6 + 7, 2) ==> A'(1, 2)

After doing the translation, we have to reflect about x-axis.

Put y = -y

A'(1, -2)

So, the required point is option c.

Problem 7 :

Which expression describes the translation of a point from (-3, 4) to (4, -1).

a) 7 units left and 5 units up.

b)  7 units right and 5 units up.

c)  7 units left and 5 units down

d)  7 units right and 5 units down.

Solution :

(-3, 4) ==> (4, -1)

(-3 + h, 4 + k) ==> (4, -1)

-3 + h = 4 and 4 + k = -1

h = 4 + 3 and k = -1 - 4

h = 7 and k = -5

Since the value of h is positive, we move right 7 units and the value of k is negative, we have to move down 5 units. So, option d is correct.

Problem 8 :

The vertices of triangle ABC are (2, 1), B (3, 4) and C(1, 3). If triangle is translated 1 unit down and 3 units left to create triangle DEF, what are the coordinated of triangle DEF?

Solution :

Original point will be in the form (x, y), after doing the translation, we get (x + h, y + k)

Based on the horizontal movement and vertical movement, we have to fix the sign of h and k.

1 unit down, so k = -1

3 units right, so h = 3

• A(2, 1) ==> A'(2 - 1, 1 + 3) ==> A'(1, 4)
• B (3, 4) ==> B'(3 - 1, 4 + 3) ==> B'(2, 7)
• C(1, 3) ==> C'(1 - 1, 3 + 3) ==> C'(0, 6)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.