TRANSVERSAL LINES

A straight line that intersects two or more straight lines at distinct points is called as transversal.

More clearly, 

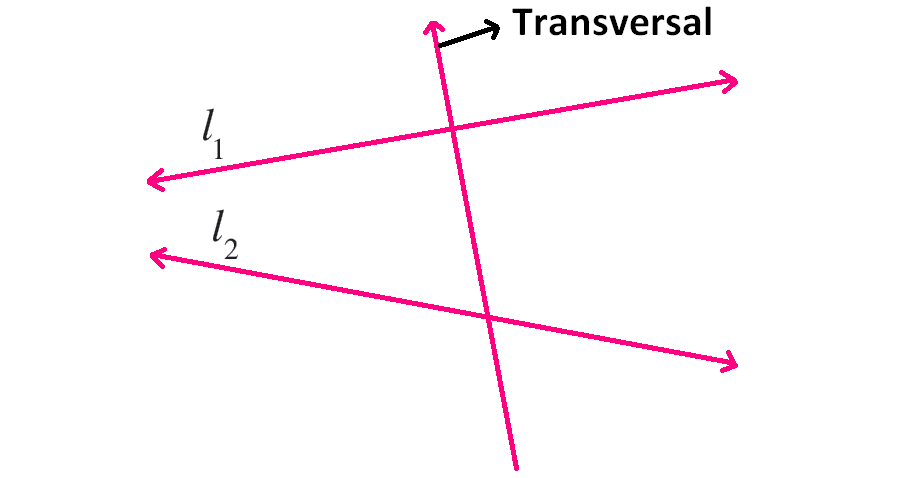
A straight line intersecting two parallel lines.

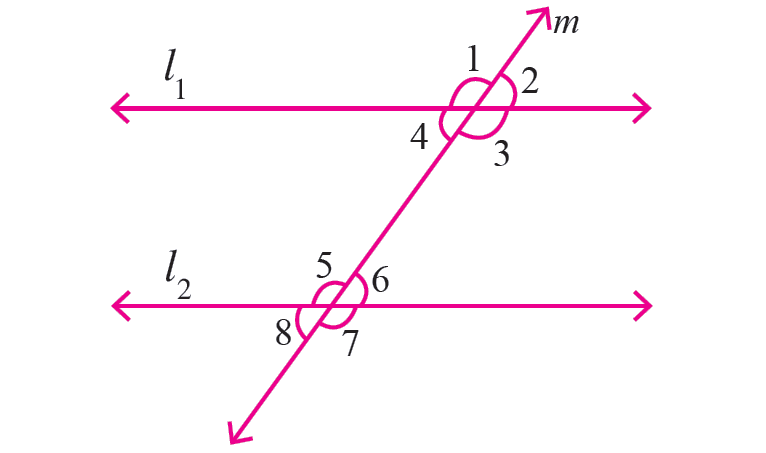
From the above figure, we have the following important points. 

Practice Problems

Problem 1 :

In the figure given below,  let the lines l₁ and l₂ be parallel and m is transversal. If ∠F  =  65°, find the measure of each of the remaining angles.  

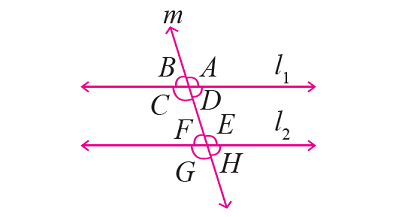
Solution : 

From the given figure, 

∠F and ∠H are vertically opposite angles and they are equal. 

Then, 

∠H  =  ∠F

∠H  =  65°

∠H and ∠D are corresponding angles and they are equal. 

Then,

∠D  =  ∠H

∠D  =  65°

∠D and ∠B are vertically opposite angles and they are equal. 

Then, 

∠B  =  ∠D

∠B  =  65°

∠F and ∠E are together form a straight angle.

Then, we have

∠F + ∠E  =  180°

Substitute ∠F  =  65°.

65° + ∠E  =  180°

∠E  =  115°

∠E and ∠G are vertically opposite angles and they are equal. 

Then,

∠G  =  ∠E

∠G  =  115°

∠G and ∠C are corresponding angles and they are equal. 

Then,

∠C  =  ∠G

∠C  =  115°

∠C and ∠A are vertically opposite angles and they are equal. 

Then,

∠A  =  ∠C

∠A  =  115°

Therefore, 

∠A  =  ∠C  =  ∠E  =  ∠G  =  115°

∠B  =  ∠D  =  ∠F  =  ∠H  =  65°

Problem 2 :

In the figure given below,  let the lines l₁ and l₂ be parallel and t is transversal. Find the value of x.

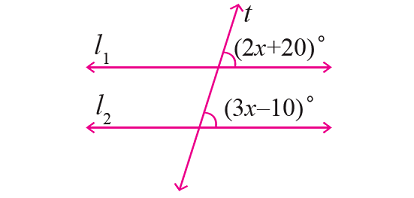
Solution : 

From the given figure, 

∠(2x + 20)° and ∠(3x - 10)° are corresponding angles. 

So, they are equal. 

Then, 

2x + 20  =  3x - 10

30  =  x

Problem 3 :

In the figure given below,  let the lines l₁ and l₂ be parallel and t is transversal. Find the value of x.

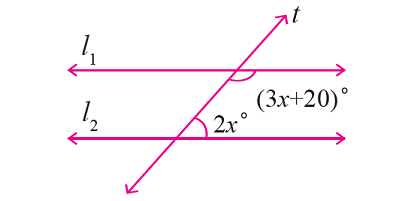
Solution : 

From the given figure, 

∠(3x + 20)° and ∠2x° are consecutive interior angles. 

So, they are supplementary. 

Then, 

3x + 20 + 2x  =  180°

5x + 20  =  180°

5x  =  160°

x  =  32°

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.