TRAPEZOIDS AND KITES WORKSHEET

Problem 1 :

Trapezoid PQRS given below is an isosceles trapezoid.

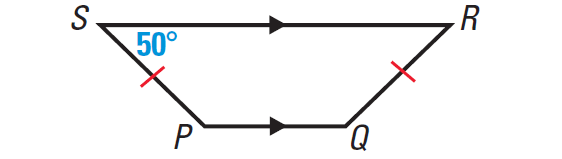
Find m∠P, m∠Q and m∠R.

Problem 2 :

Prove that the figure ABCD given below is a trapezoid.

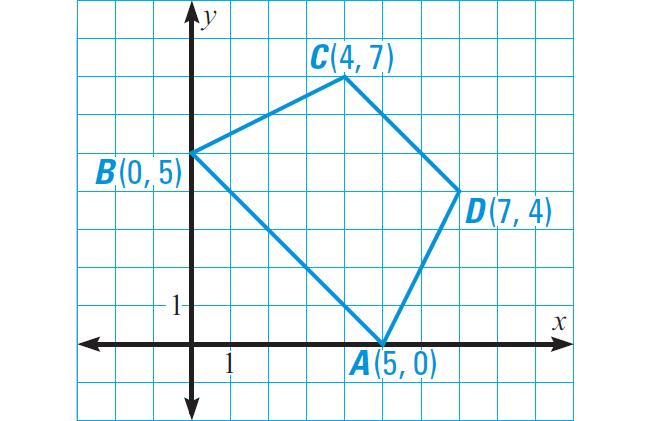
Problem 3 :

A baker is making a cake like the one which is given below. The top layer of the cake has a diameter of 8 inches and the bottom layer has a diameter of 20 inches. How big should the middle layer of the cake be?

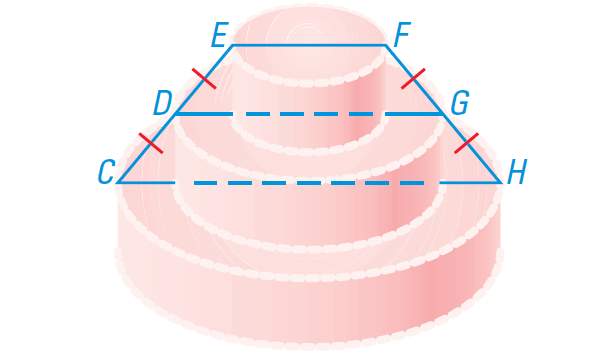
Problem 4 :

In the kite WXYZ shown below, find the length of each side.

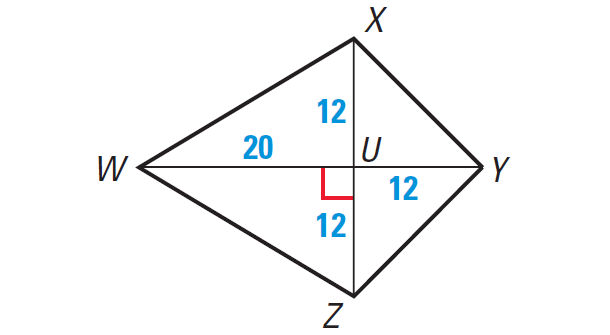
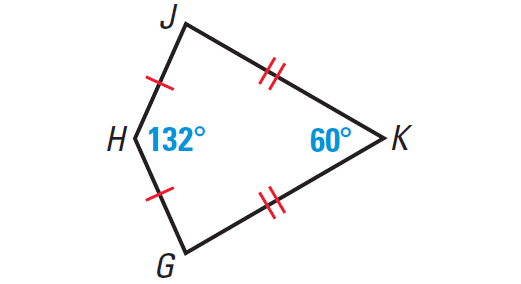
Problem 5 :

Find m∠G and m∠J in the diagram shown below.

1. Answer :

Given : PQRS is an isosceles trapezoid.

According to theorem on trapezoids, each pair of base angles in an isosceles trapezoid must be congruent.

So, we have

m∠S = m∠R = 50°

Because ∠S and ∠P are consecutive interior angles formed by parallel lines, they are supplementary.

So, we have

m∠S + m∠P = 180°

Substitute m∠S = 50°.

50° + m∠P = 180°

Subtract 50° from both sides.

m∠P = 130°

According to theorem on trapezoids, each pair of base angles in an isosceles trapezoid must be congruent.

So, we have

m∠P = ∠Q = 130°

Hence,

m∠P = 130°

m∠Q = 130°

m∠R = 50°

2. Answer :

Find the slope of each side of the figure ABCD above and compare the slopes of opposite sides.

We can find the slope using slope formula given below.

Slope of the line joining two points (x₁, y₁) and (x₂, y₂) :

Slope of AB = (5 - 0)/(0 - 5) = 5/(-5) = -1

Slope of CD = (4 - 7)/(7 - 4) = -3/3 = -1

Because the slopes of AB and CD are equal, we have

AB || CD

Slope of BC = (7 - 5)/(4 - 0) = 2/4 = 1/2

Slope of AD = (4 - 0)/(7 - 5) = 4/2 = 2

The slopes of BC and AD are not equal. So BC and AD are not parallel.

Because AB ∥ CD and BC ∦ AD, ABCD is a trapezoid.

3. Answer :

In the diagram given above, EFCH is an isosceles trapezoid and DG is the midsegment of the trapezoid.

And also, DG is the diameter of middle layer of the cake. 

Using the Midsegment Theorem for Trapezoids, we have

DG = 1/2 ⋅ (EF + CH)

= 1/2 ⋅ (8 + 20)

= 1/2 ⋅ (28)

= 14

Hence, the diameter of the middle layer of the cake is 14 inches.

4. Answer :

Because WXYZ is a kite, the diagonals are perpendicular. We can use Pythagorean theorem to find the side lengths.

In the kite WXYZ shown above, let us consider the triangle part WUZ.

Because the diagonals WY and XZ are perpendicular and they intersect at U, angle U is a right angle.

So, WUZ is a right triangle.

By Pythagorean theorem, we have

WZ² = WU² + UZ²

Take radical on both sides.

√WZ² = √(WU² + UZ²)

WZ = √(20² + 12²)

WZ = √(400 + 144)

WZ = 544

WZ ≈ 23.32

Similarly, in the right triangle triangle YUZ, we have

YZ² = YU² + UZ²

Take radical on both sides.

√YZ² = √(YU² + UZ²)

YZ = √(12² + 12²)

YZ = √(144 + 144)

YZ = √288

YZ ≈ 16.97

We know that a kite is  a quadrilateral that has two pairs of consecutive congruent sides, but opposite sides are not congruent.

So, in the kite WXYZ shown above, we have

WX ≅ WZ

YX ≅ YZ

Hence, we have

WX = WZ ≈ 23.32

YX = YZ ≈ 16.97

5. Answer :

The quadrilateral GHJK shown above has two pairs of consecutive congruent sides, but opposite sides are not congruent.

So, the quadrilateral GHJK is a kite.

By theorem, exactly one pair of opposite angles of a kite are congruent.

But, in the diagram shown above, the pair of m∠H and m∠K are not congruent.

Then, the pair of m∠G and m∠J must be congruent.

That is,

m∠G ≅ m∠J

Let, m∠G = m∠J = x°.

We know that the four angles of a quadrilateral add up to 360°.

So, we have

m∠G + m∠H + m∠J + m∠K = 360°

x° + 132° + x° + 60° = 360°

Simplify.

2x° + 192°  =  360°

Subtract 192° from both sides.

2x° + 192° = 360°

2x° = 168°

Divide both sides by 2.

x° = 84°

Hence, we have

m∠G = m∠J = 84°

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.