TRAPEZOIDS AND KITES

Trapezoids

A trapezoid is a quadrilateral with exactly one pair of parallel sides. The parallel sides are the bases. A trapezoid has two pairs of base angles.

For instance, in the trapezoid PQRS given below ∠S and ∠R.

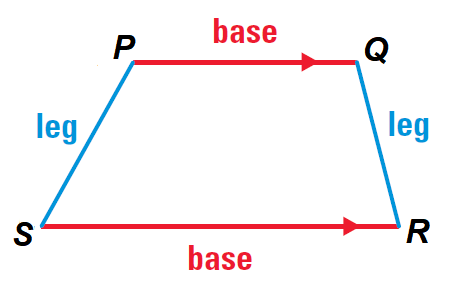
The other pair is ∠P and ∠Q. The non parallel sides are the legs of the trapezoid.

If the legs of a trapezoid are congruent, then the trapezoid is an isosceles trapezoid.

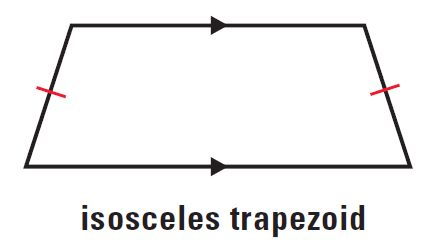
Kites

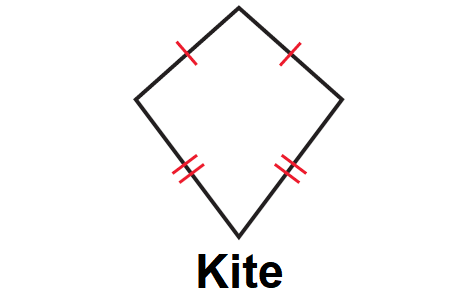
A kite is a quadrilateral that has two pairs of consecutive congruent sides, but opposite sides are not congruent.

Theorems on Trapezoids

Theorem 1 :

If a trapezoid is isosceles, then each pair of base angles is congruent.

It has been illustrated in the diagram given below.

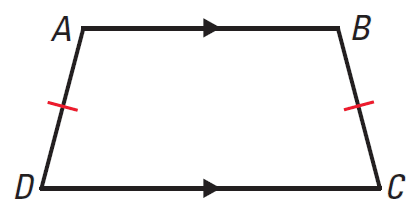
In the trapezoid ABCD above, we have

∠A ≅ ∠B,  ∠C ≅ ∠D

Theorem 2 :

If a trapezoid has a pair of congruent base angles, then it is an isosceles trapezoid.

It has been illustrated in the diagram given below.

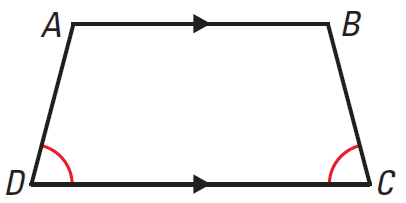
Trapezoid ABCD given above is an isosceles trapezoid. Because the base angles are congruent.

That is,

∠D ≅ ∠C

Theorem 3 :

A trapezoid is isosceles if and only if its diagonals are congruent.

It has been illustrated in the diagram given below.

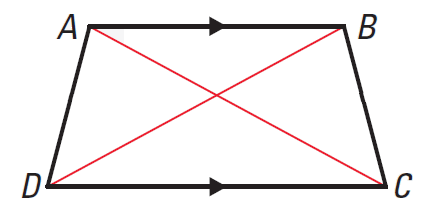
The trapezoid ABCD above can be isosceles, if and only if

AC ≅ BD

Midsegment of a Trapezoid

The midsegment of a trapezoid is the segment that connects the midpoints of its legs.

It has been illustrated in the diagram given below.

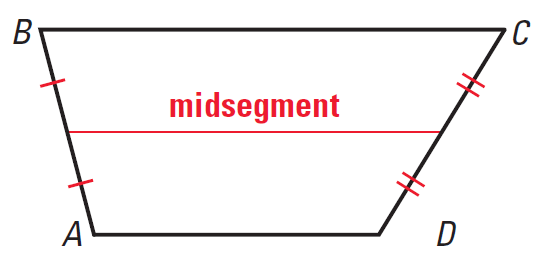
Midsegment Theorem for Trapezoids

The midsegment of a trapezoid is parallel to each base and its length is one half the sum of the lengths of the bases.

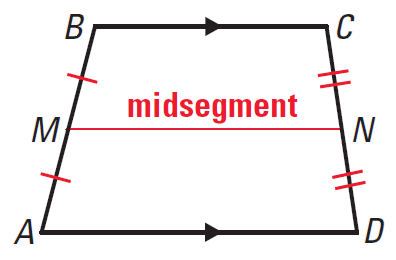
In the trapezoid ABCD given above, according to Midsegment Theorem for Trapezoids, we have

MN || AD

MN || BC

MN = 1/2 ⋅ (AD + BC)

Theorems on Kites

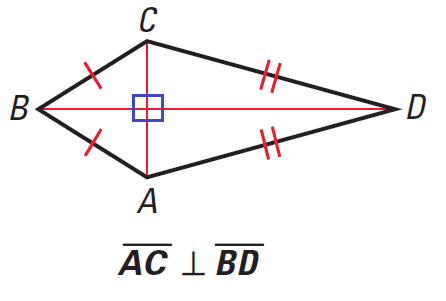
Theorem 1 :

If a quadrilateral is a kite, then its diagonals are perpendicular.

It has been illustrated in the diagram shown below.

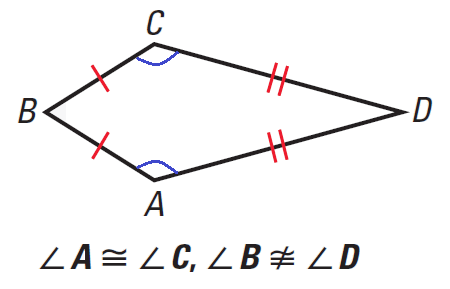
Theorem 2 :

If a quadrilateral is a kite, then exactly one pair of opposite angles are congruent.

It has been illustrated in the diagram shown below.

Problem 1 :

Find the area of the following.

Solution :

Area of trapezium = (1/2) x height x (base 1 + base 2)

base 1 = 3 + 6 + 2 ==> 11

Base 2 = 6

height = 6√2

= (1/2) x 6√2 x (11 + 6)

= 3√2 x 17

= 51 √2 square units.

Problem 2 :

The median is equal to 25 cm and the height is 8 cm.

Solution :

Length of median = (1/2) (base 1 + base 2)

length of median = 25 cm

25 = (1/2) (base 1 + base 2)

Base 1 + base 2 = 25(2)

= 50 cm

Height = 8 cm

ARea of trapezoid = (1/2) x 8 x 50

= 4 x 50

= 200 square cm

Problem 3 :

The area of the trapezoid is 75 square inches and its two bases are 8 and 17 inches long. Find the height of the trapezoid.

Solution :

Area of trapezoid = 75 square inches

lenght of bases = 8 inches and 17 inches

height = ?

75 = (1/2) x height x (8 + 17)

75 = (1/2) x height x 25

height = 75(2)/25

= 6 inches

So, the height of the trapezium is 6 inches.

Problem 4 :

The length of one of the diagonals of a kite is 4 cm longer than twice the length of the other diagonal. Find the area of kite is 15 cm^2. Find the length of the diagonal.

Solution :

Let x be the length of one diagonal.

Lenght of other diagonal = 2x + 4

Area of kite = 15 cm^2

Area of kite = (1/2) x diagona 1 x diagonal 2

15 = (1/2)  x(2x + 4)

30 = 2x^2 + 4 x

2x^2 + 4 x - 30 = 0

x^2 + 2 x - 15 = 0

(x + 5)(x - 3) = 0

x = -5 and x = 3

2x + 4 ==> 2(3) + 4

= 6 + 4

= 10 cm

So, the length of the diagonals are 3 cm and 10 cm respectively.

Problem 5 :

Solve for x.

Solution :

50 = 8x + 2

50 - 2 = 8x

8x = 48

x = 48/8

x = 6

Problem 6 :

ME = 20, find MK.

Solution :

MK = 2(ME)

= 2(20)

= 40

Problem 7 :

The lengths of the bases of an isosceles trapezoid are shown below.

If the perimeter of the trapezoid is 32 units, what is the area ?

a)  44 square units        b) 110 square units

c)  88 square units       d)  55 square units

Solution :

perimeter of the trapezoid = 32 units

Sum of lengths of two sides = 32 - (14 + 8)

= 32 - 22

= 10 units

Side length of isosceles trapezium = 5 units

(height of the trapezium)^2 + 3^2 = 5^2

(height of the trapezium)^2 + 9 = 25

(height of the trapezium)^2 = 25 - 9

(height of the trapezium)^2 = 16

height of trapezium = √16 ==> 4

Area of trapezium = (1/2) x 4 x (8 + 14)

=  (1/2) x 4 x 22

= 44 square units

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.