TRAPEZOIDS

A trapezoid is a quadrilateral with exactly one pair of parallel sides. The parallel sides are the bases. A trapezoid has two pairs of base angles.

For instance, in the trapezoid PQRS given below ∠S and ∠R.

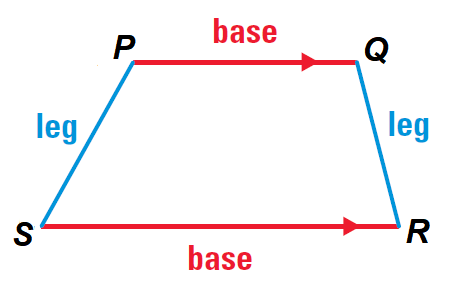
The other pair is ∠P and ∠Q. The non parallel sides are the legs of the trapezoid.

If the legs of a trapezoid are congruent, then the trapezoid is an isosceles trapezoid.

Theorems on Trapezoids

Theorem 1 :

If a trapezoid is isosceles, then each pair of base angles is congruent.

It has been illustrated in the diagram given below.

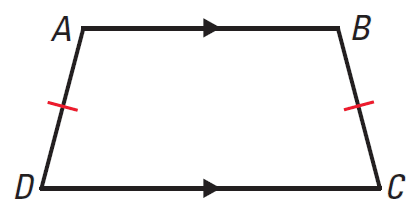
In the trapezoid ABCD above, we have

∠A ≅ ∠B,  ∠C ≅ ∠D

Theorem 2 :

If a trapezoid has a pair of congruent base angles, then it is an isosceles trapezoid.

It has been illustrated in the diagram given below.

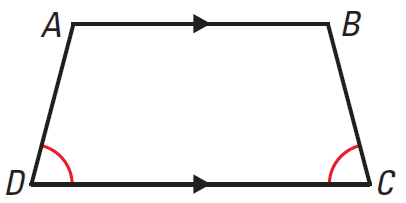
Trapezoid ABCD given above is an isosceles trapezoid. Because the base angles are congruent.

That is,

∠D ≅ ∠C

Theorem 3 :

A trapezoid is isosceles if and only if its diagonals are congruent.

It has been illustrated in the diagram given below.

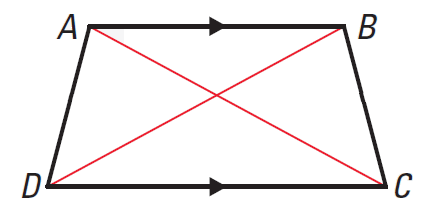
The trapezoid ABCD above can be isosceles, if and only if

AC ≅ BD

Midsegment of a Trapezoid

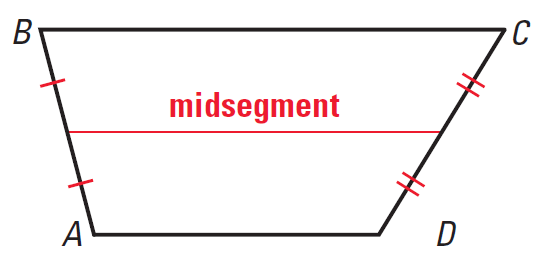
The midsegment of a trapezoid is the segment that connects the midpoints of its legs.

It has been illustrated in the diagram given below.

Midsegment Theorem for Trapezoids

The midsegment of a trapezoid is parallel to each base and its length is one half the sum of the lengths of the bases.

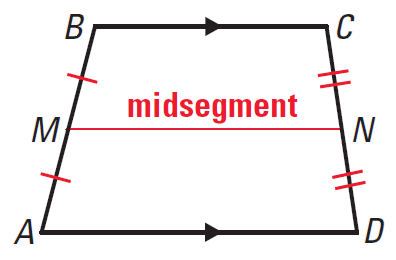
In the trapezoid ABCD given above, according to Midsegment Theorem for Trapezoids, we have

MN || AD

MN || BC

MN = 1/2 ⋅ (AD + BC)

Solved Problems

Problem 1 :

Trapezoid PQRS given below is an isosceles trapezoid.

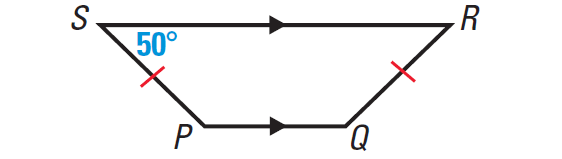
Find m∠P, m∠Q and m∠R.

Solution :

Given : PQRS is an isosceles trapezoid.

According to theorem 1 above, each pair of base angles in an isosceles trapezoid must be congruent.

So, we have

m∠S = m∠R = 50°

Because ∠S and ∠P are consecutive interior angles formed by parallel lines, they are supplementary.

So, we have

m∠S + m∠P = 180°

Substitute m∠S = 50°.

50° + m∠P = 180°

Subtract 50° from both sides.

m∠P = 130°

According to theorem 1 above, each pair of base angles in an isosceles trapezoid must be congruent.

So, we have

m∠P = ∠Q = 130°

Hence,

m∠P = 130°

m∠Q = 130°

m∠R = 50°

Problem 2 :

Prove that the figure ABCD given below is a trapezoid.

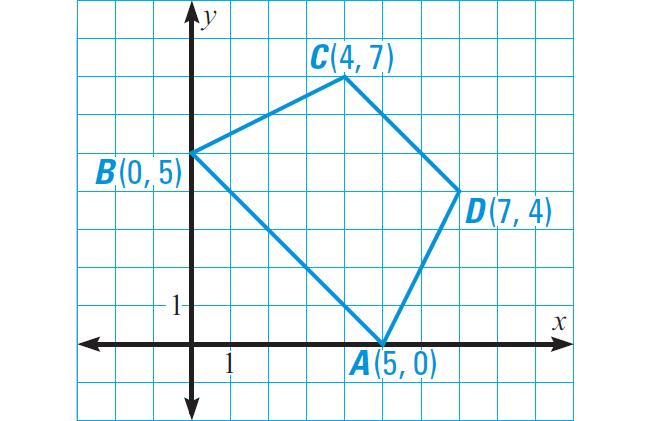
Solution :

Find the slope of each side of the figure ABCD above and compare the slopes of opposite sides.

We can find the slope using slope formula given below.

Slope of the line joining two points (x₁, y₁) and (x₂, y₂) :

Slope of AB = (5 - 0)/(0 - 5) = 5/(-5) = -1

Slope of CD = (4 - 7)/(7 - 4) = -3/3 = -1

Because the slopes of AB and CD are equal, we have

AB || CD

Slope of BC = (7 - 5)/(4 - 0) = 2/4 = 1/2

Slope of AD = (4 - 0)/(7 - 5) = 4/2 = 2

The slopes of BC and AD are not equal. So BC and AD are not parallel.

Because AB ∥ CD and BC ∦ AD, ABCD is a trapezoid.

Problem 3 :

A baker is making a cake like the one which is given below. The top layer of the cake has a diameter of 8 inches and the bottom layer has a diameter of 20 inches. How big should the middle layer of the cake be?

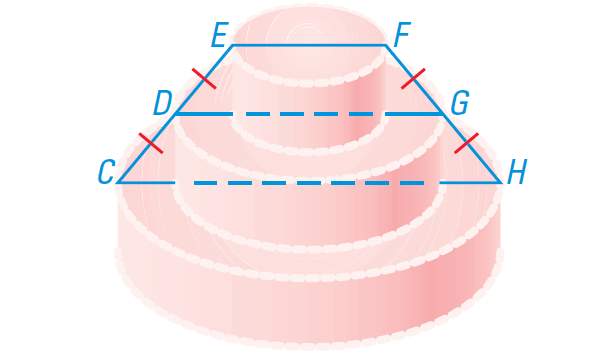
Solution :

In the diagram given above, EFCH is an isosceles trapezoid and DG is the midsegment of the trapezoid.

And also, DG is the diameter of middle layer of the cake.

Using the Midsegment Theorem for Trapezoids, we have

DG = 1/2 ⋅ (EF + CH)

= 1/2 ⋅ (8 + 20)

= 1/2 ⋅ (28)

= 14

Hence, the diameter of the middle layer of the cake is 14 inches.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.