TRIANGLE PROPORTIONALITY THEOREM WORKSHEET

Problems 1-3 : Find the missing length indicated.

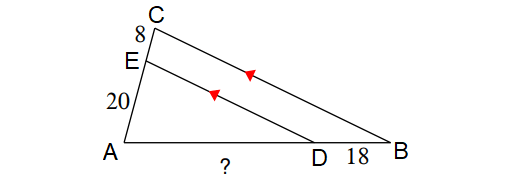
Problem 1 :

Problem 2 :

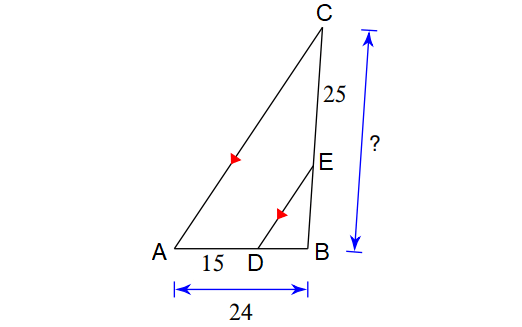
Problem 3 :

Problem 4 :

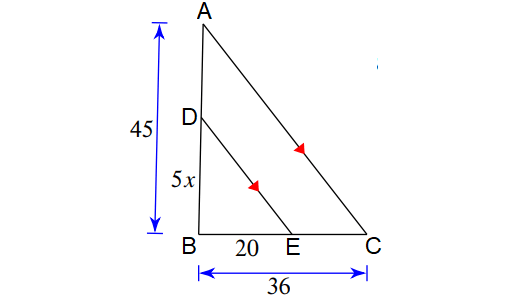
Solve for x.

Problem 5 :

Solve for x.

Problem 6 :

Solve for x.

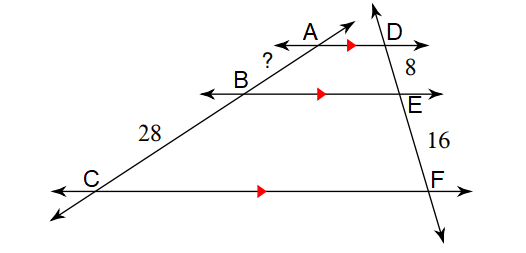
Problem 7 :

Solve for x.

1. Answer :

In the triangle shown above, line segment ED is parallel to the side BD.

By Triangle Proportionality Theorem,

AD/DB = AE/EC

Substitute.

AD/18 = 20/8

AD/18 = 5/2

Multiply both sides by 18.

AD = 45

2. Answer :

In the triangle shown above, line segment ED is parallel to the side AC.

By Triangle Proportionality Theorem,

BE/EA = BD/DC

15/EA = (BC - DC)/DC

Substitute.

15/EA = (14 - 4)/4

15/EA = 10/4

15/EA = 5/2

Take reciprocal on both sides.

EA/15 = 2/5

Multiply both sides by 15.

EA = 6

3. Answer :

In the triangle shown above, line segment ED is parallel to the side AC.

By Triangle Proportionality Theorem,

BD/DA = BE/EC

(BA - DA)/DA = BE/EC

Substitute.

(24 - 15)/15 = BE/25

9/15 = BE/25

3/5 = BE/25

Multiply both sides by 25.

BE = 15

BC = BE + EC

= 15 + 25

= 40

4. Answer :

In the triangle shown above, line segment ED is parallel to the side AC.

By Triangle Proportionality Theorem,

BD/DA = BE/EC

BD/(BA - DA) = BE/EC

BD/(BA - DA) = BE/(BC - BE)

Substitute.

5x/(45 - 5x) = 20/(36 - 20)

5x/(45 - 5x) = 20/16

5x/(45 - 5x) = 5/4

4(5x) = 5(45 - 5x)

20x = 225 - 25x

Add 25x to both sides.

45x = 225

Divide both sides by 45.

x = 5

5. Answer :

In the diagram above, line segments AD, BE and CF are parallel to each other.

By Theorem,

AB/BC = DE/EF

Substitute.

AB/28 = 8/16

AB/28 = 1/2

Multiply both sides by 28.

AB = 14

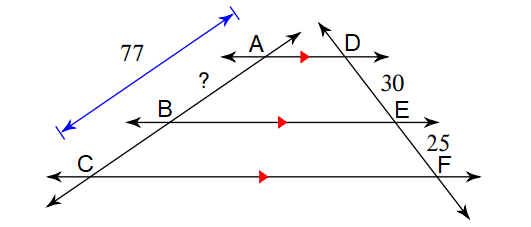
6. Answer :

In the diagram above, line segments AD, BE and CF are parallel to each other.

By Theorem,

AB/AC = DE/DF

AB/AC = DE/(DE + EF)

Substitute.

AB/77 = 30/(30 + 25)

AB/77 = 30/55

AB/77 = 6/11

Multiply both sides by 77.

AB = 42

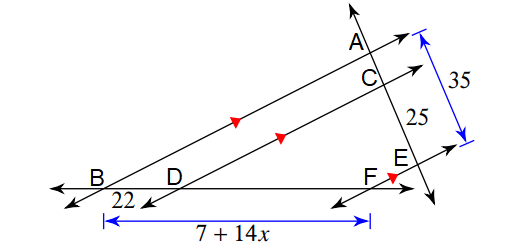
7. Answer :

In the diagram above, line segments AB, CD and EF are parallel to each other.

By Theorem,

AC/BD = CE/DF

(AE - CE)/BD = CE/(BF - BD)

Substitute.

(35 - 25)/22 = 25/(7 + 14x - 22)

10/22 = 25/(14x - 15)

5/11 = 25/(14x - 15)

5(14x - 15) = 11(25)

70x - 75 = 275

Add 75 to both sides.

70x = 350

Divide both sides by 70.

x = 5

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.