TRIANGLE SUM THEOREM
The sum of the measures of the interior angles of a triangle is 180°.
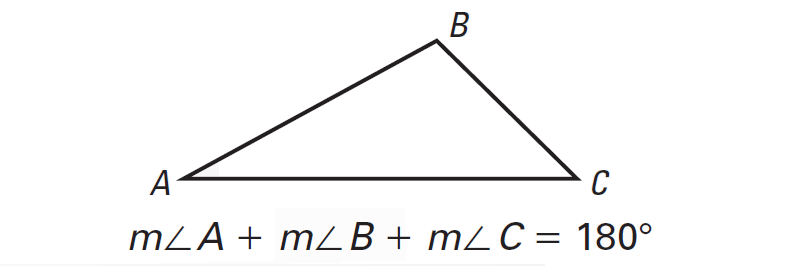
Proof :
Given :
Triangle ABC.
To Prove :
m∠1 + m∠2 + m∠3 = 180°
Plan for Proof :
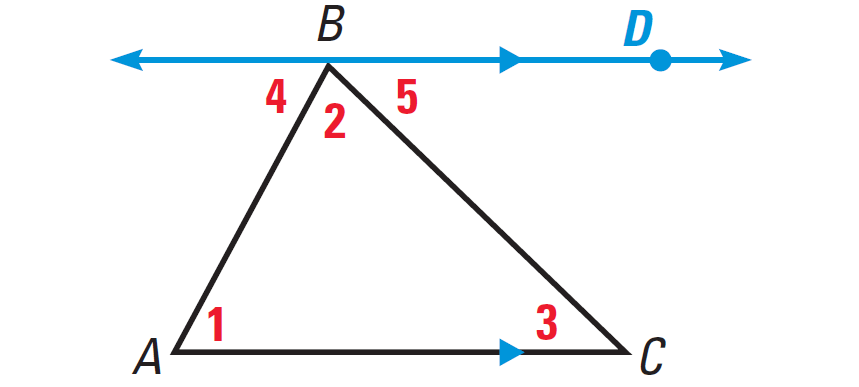
By the Parallel Postulate, we can draw an auxiliary line through point B and parallel to AC. Because ∠4, ∠2 and ∠5 form a straight angle, the sum of their measures is 180°.
We also know that ∠1 ≅ ∠4 and ∠3 ≅ ∠5 by the Alternate Interior Angles Theorem.
|
Statements Draw BD parallel to AC m∠4 + m∠2 + m∠5 = 180° ∠1 ≅ ∠4 and ∠3 ≅ ∠5 |
Reasons Parallel Postulate Angle addition postulate and definition of straight angle. Alternate Interior Angles Theorem |
|
m∠1 = m∠4 and m∠3 = m∠5 |
Definition of congruent angles. |
|
m∠1 + m∠2 + m∠3 = 180° |
Substitution property of equality. |
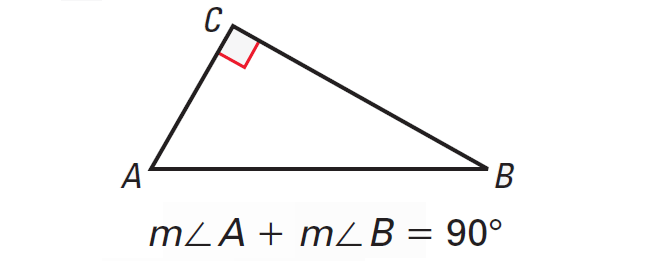
Corollary to the Triangle Sum Theorem
The acute angles of a right triangle are complementary.
Example 1 :
Can 30°, 60° and 90° be the angles of a triangle ?
Solution :
Let us add all the three given angles and check whether the sum is equal to 180°.
30° + 60° + 90° = 180°
The sum of the three angles is equal 180°. By Triangle Sum Theorem, the given three angles can be the angles of a triangle.
Example 2 :
Find the missing angles in the triangle shown below.
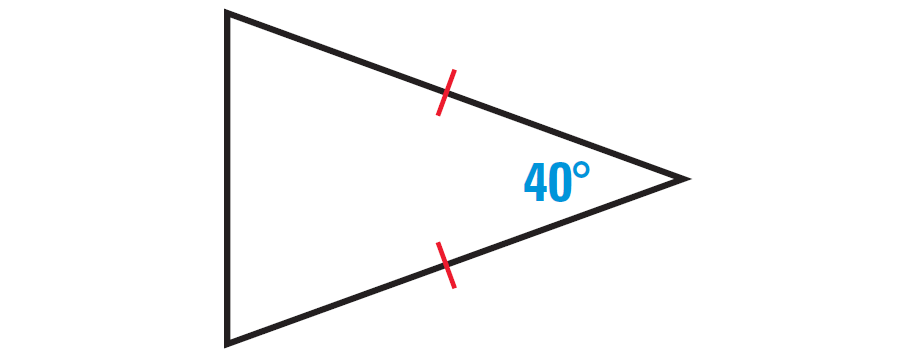
Solution :
In the triangle shown above, two sides are congruent. Angles opposite to congruent sides are always congruent.
So, if one missing angle is assumed to be x°, then the other missing angle also must be x°. Because the two angles are congruent.
The diagram shown below illustrates this.
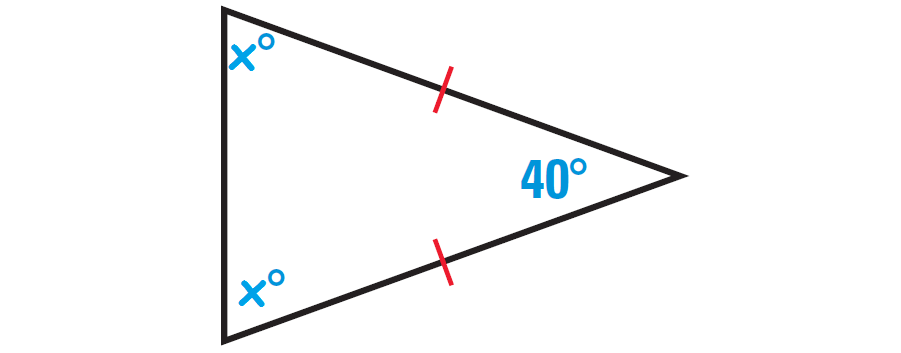
By Triangle Sum Theorem, the sum of the measures of the interior angles of a triangle is 180°.
So, we have
x° + x° + 40° = 180°
Simplify.
2x + 40 = 180
Subtract 40 from both sides.
2x = 140
Divide both sides by 2.
x = 70
The measure of each missing angle is 70°.
Example 3 :
The measure of one acute angle of a right triangle is two times the measure of the other acute angle. Find the measure of each acute angle.
Solution :
Let A, B and C be the vertices of the triangle and right angle is at C.
Let ∠A = x°, then ∠B = 2x°. The diagram shown below illustrates this.
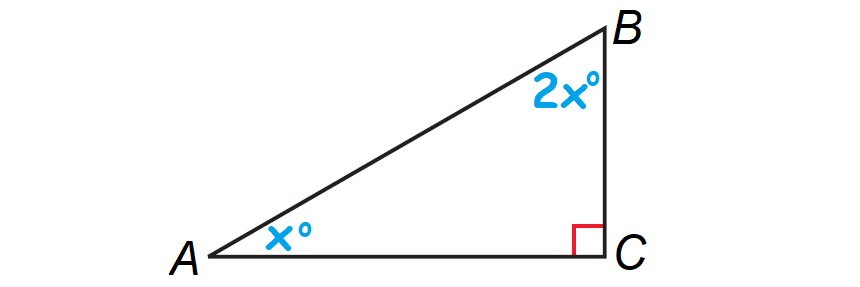
By Corollary to the Triangle Sum Theorem, the acute angles of a right triangle are complementary.
So, we have
x° + 2x° = 90°
Simplify.
3x° = 90°
Divide both sides by 3.
x = 30
m∠A = 30°
m∠B = 2(30°) = 60°
The two acute angles are 30° and 60°.
Example 4 :
Find the missing angles in the triangle shown below.
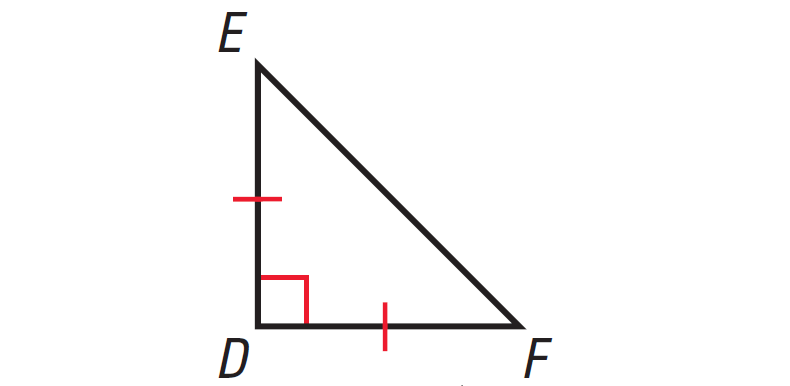
Solution :
In the triangle shown above, two sides are congruent. Angles opposite to congruent sides are always congruent.
So, if one missing angle is assumed to be x°, then the other missing angle also must be x°. Because the two angles are congruent.
The diagram shown below illustrates this.
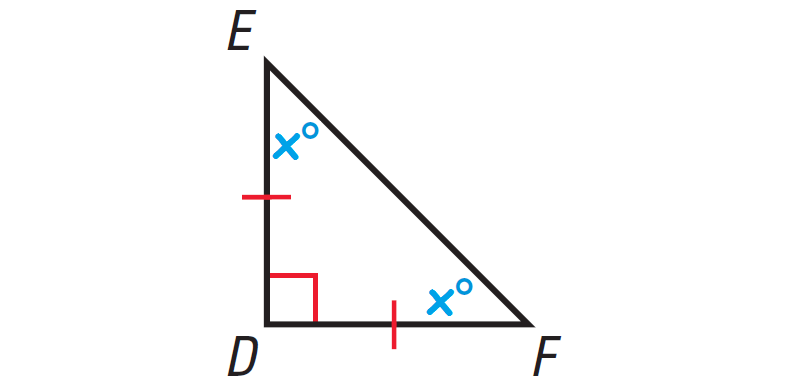
In the triangle shown above, one of the angles is right angle. So, it is right triangle.
By Corollary to the Triangle Sum Theorem, the acute angles of a right triangle are complementary.
So, we have
x° + x° = 90°
Simplify.
2x = 90
Divide both sides by 2.
x = 45
The measure of each missing angle is 45°.
Example 5 :
In a triangle, If the second angle is 5° greater than the first angle and the third angle is 5° greater than second angle, find the three angles of the triangle.
Solution :
Let "x°" be the first angle.
The second angle = (x + 5)°
The third angle = x + 5 + 5 = (x + 10)°
We know that,
the sum of the three angles of a triangle = 180°
x + (x+5) + (x+10) = 180
3x + 15 = 180
3x = 165
x = 55
- The first angle = 55°
- The second angle = 55 + 5 = 60°
- The third angle = 60 + 5 = 65°
The three angles of a triangle are 55°, 60° and 65°.
Example 6 :
If the angles of a triangle are in the ratio 2 : 7 : 11, then find the angles.
Solution :
From the ratio 2 : 7 : 11, the three angles are 2x, 7x, 11x.
In any triangle, sum of the angles = 180°
So, we have
2x + 7x + 11x = 180
20x = 180 -------> x = 9
- Then, the first angle = 2x = 2(9) = 18°
- The second angle = 7x = 7(9) = 63°
- The third angle = 11x = 11(9) 99°
The angles of the triangle are 18°, 63° and 99°.
Example 7 :
Find the value of x.
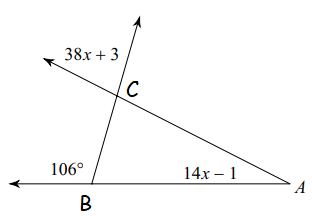
Solution :
<BCA = 38x + 3 (Vertical angles will be equal)
106 + <CBA = 180 (linear pair)
<CBA = 180 - 106
<CBA = 74
Sum of interior angles will be equal to 180.
<CBA + <BCA + <BAC = 180
74 + 38x + 3 + 14x - 1 = 180
52x + 77 - 1 = 180
52x + 76 = 180
52x = 180 - 76
52x = 104
x = 104/52
x = 2
So, the value of x is 2.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 145)
Apr 16, 25 12:35 PM
Digital SAT Math Problems and Solutions (Part - 145) -
Digital SAT Math Problems and Solutions (Part - 144)
Apr 14, 25 07:27 PM
Digital SAT Math Problems and Solutions (Part - 144) -
Quadratic Equation Problems with Solutions (Part - 1)
Apr 14, 25 11:33 AM
Quadratic Equation Problems with Solutions (Part - 1)

