HOW TO FIND AREA OF TRIANGLE USING COORDINATES

Find the area of the triangle formed by the points.

Problem 1 :

(0, 0), (3, 0) and (0, 2)

Solution :

Let A(0, 0) , B(3, 0) and C(0, 2) be the vertices of the triangle taken in order.

x₁ = 0          x₂ = 3         x₃ = 0

y₁ = 0          y₂ = 0         y₃ = 2

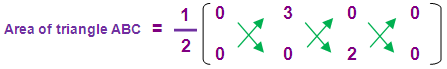
Area of the triangle triangle ABC :

  =  (1/2)[(0 + 6 + 0) – (0 + 0 + 0)]

  =  (1/2)[6 - 0]

  =  (1/2)[6]

  =  3 square units

Problem 2 :

(5, 2) (3, -5) and (-5, -1)

Solution :

Let A (-5, -1), B (3, -5) and C (5, 2) be the vertices of the triangle taken in order.

x₁ = -5          x₂ = 3         x₃ = 5

y₁ = -1          y₂ = -5         y₃ = 2

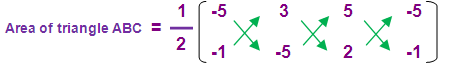
Area of the triangle ABC :

  =  (1/2)[(25 + 6 - 5) – (-3 - 25 - 10)]

  =  (1/2)[(31 - 5) –(-38)]

  =  (1/2)[26 +38]

  =  (1/2)[64]

  =  32 square units

Problem 3 :

(-4, -5), (4, 5) and (-1, -6)

Solution :

Let A(-4, -5) , B(-1, -6) and C(4, 5) are the vertices of the triangle taken in order.

x₁ = -4          x₂ = -1         x₃ = 4

y₁ = -5          y₂ = -6         y₃ = 5

Area of the triangle ABC :

  =  (1/2)[(24 - 5 - 20) – (5 - 24 - 20)]

  =  (1/2)[(24 - 25) –(5 - 44)]

  =  (1/2)[(-1) – (-39)]

  =  (1/2)[-1 + 39]

  =  (1/2)[38]

  =  19 square units

Problem 4 :

Given the triangle below with vertices 𝐴(−2, 3), 𝐵(4, 4), and 𝐶(−1, −2). Calculate its area.

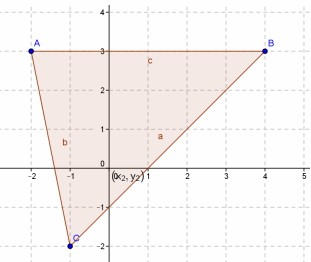
By observing the figure above, we can find the vertical distance between from C to AB.

Height = 5 units.

Distance between AB = √(y₂ - y₁)² + (x₂ - x₁)²

𝐴(−2, 3), 𝐵(4, 4),

= √(4 - 3)² + (4 - (-2))²

= √1² + (4 + 2)²

Base = √37

Area of triangle = (1/2) x √37 x 5

= 5/2√37 square cm.

Problem 5 :

Draw Triangle ∆𝑉𝐸𝑋 that has vertices 𝑉(−5, 2), 𝐸(−11, −1) 𝑎𝑛𝑑 𝑋(−3, −1).

a. Find the perimeter of ∆𝑉𝐸X

b. Find the area of ∆𝑉𝐸X

Solution :

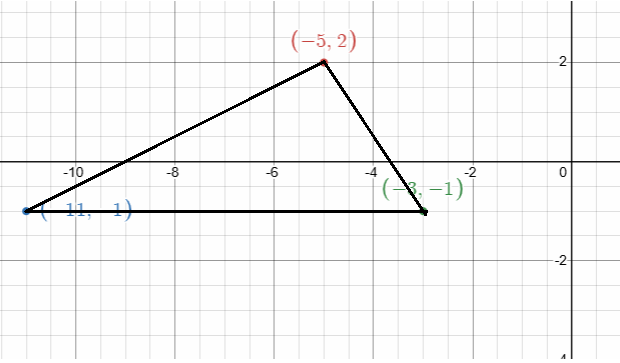
a) Finding the perimeter :

Distance between two points  = √(y₂ - y₁)² + (x₂ - x₁)²

𝑉(−5, 2), 𝐸(−11, −1)

Length of VE = √(-1 - 2)² + (-11 + 5)²

= √(-3)² + (-6)²

= √9 + 36

= √45

= 3√5

𝐸(−11, −1) 𝑋(−3, −1).

Length of EX = √(-1 + 1)² + (-3 + 11)²

= √0² + 8²

= √64

= 8

𝐸(−11, −1) 𝑋(−3, −1).

𝑉(−5, 2) and 𝑋(−3, −1).

Length of EX = √(-1 - 2)² + (-3 + 5)²

= √(-3)² + 2²

= √9+4

= √13

perimeter of triangle VEX = VE + EX + XV

= (3√5 + 8 + √13) units

b)  Finding the area of triangle VEX :

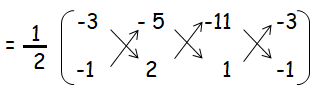
= 1/2{(-6 - 5 + 11) - (5 - 22 - 3)}

= (1/2) {(0 - (-20))

= 1/2(20)

= 10 square units.

Problem 6 :

Find the area of the triangle given below.

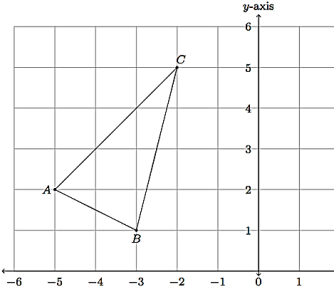
Solution :

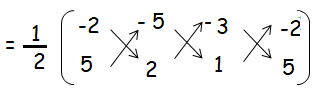
= 1/2 {(-4 - 5 - 15) - (-25 - 6 - 2)}

= (1/2) {(-24 - (-33))}

= (1/2) {(-24 + 33)}

= (1/2) {9}

= 4.5 square units.

So, the required area of the triangle above is 4.5 square units.

Problem 7 :

Find the area of the triangle given below.

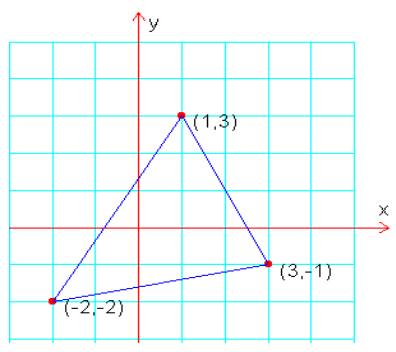
Let A (1, 3), B(-2, -2) and C(3, -1).

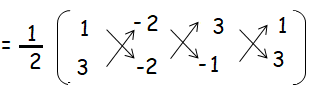
= (1/2) {(-2 + 2 + 9) - (-6 - 6 - 1)}

= (1/2) {9 - (-13)}

= (1/2)(9 + 13)

= 1/2 (22)

= 11 square units.

So, the required area of the triangle is 11 square units.

Problem 8 :

If the area of the triangle formed by the vertices A(-1 2), B (k ,-2) and C(7, 4) (taken in order) is 22 sq. units, find the value of k.

Solution :

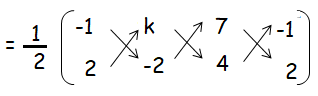
Area of the triangle = 22 square units.

(1/2){(4 + 4k + 14) - (2k - 14 - 4)} = 22

(18 + 4k) - (2k - 18) = 22(2)

18 + 4k - 2k + 18 = 44

36 + 2k = 44

2k = 44 - 36

2k = 8

k = 8/2

k = 4

So, the value of k is 4.

Find the area of the shaded region

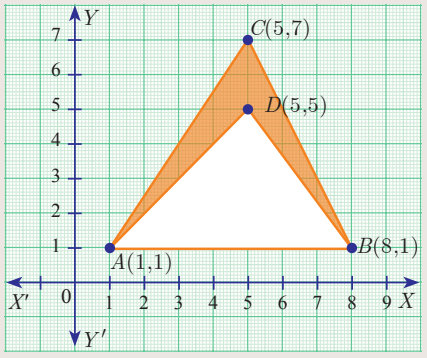
A(1, 1) B(8, 1) and C(5, 7)

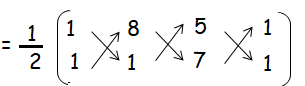
Area of triangle ABC = (1/2) {(1 + 56 + 5) - (8 + 5 + 7)}

= (1/2){62 - 20}

= (1/2) (42)

= 42/2

Area of triangle ABC = 21 square units.

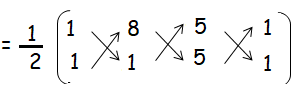
Area of triangle ABD = (1/2) {(1 + 40 + 5) - (8 + 5 + 5)}

= (1/2){46 - 18}

= (1/2) (28)

= 28/2

Area of triangle ABD = 14 square units.

Area of the shaded region = Area of triangle ABC - Area of triangle ABD

= 21 - 14

= 7 square units.

So, the area of the shaded region is 7 square units.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.