TRIANGLE WORKSHEET SOLUTION 3

3. Determine if the following set of points are collinear or not.

(i)  (4, 3), (1, 2) and (-2, 1)

Solution :

Let A(4, 3), B(1, 2) and C(-2, 1) be the vertices of the triangle.

If the three points are collinear then area of triangle will be zero

x₁ = 4          x₂ = 1         x₃ = -2

y₁ = 3          y₂ = 2         y₃ = 1

=  (1/2)[(8 + 1 – 6) – (3 - 4 + 4)]

=  (1/2)[3 – 3]

=  0

Hence the given points are collinear.

(ii) (-2, -2), (-6, -2) and (-2, 2)

Solution :

Let A (-2,-2) B (-6,-2) and C (-2,2) are the vertices of the triangle

If the three points are collinear then area of triangle will be zero

x₁ = -2          x₂ = -6         x₃ = -2

y₁ = -2          y₂ = -2         y₃ = 2

  =  (1/2)[(4 - 12 + 4) – (12 + 4 - 4)]

  =  (1/2)[-4 – 12]

  =  (1/2)(-16)

  =  -8  ≠  0

Hence the given points are not collinear.

(iii) (-3/2, 3) (6, -2) and (-3, 4)

Solution :

Let A (-3/2,3) B (6,-2) and C (-3,4) are the vertices of the triangle

If the three points are collinear then area of triangle will be zero

x₁ = -3/2          x₂ = 6         x₃ = -3

y₁ = 3          y₂ = -2         y₃ = 4

  =  (1/2)[(3 + 24 - 9) – (18 + 6 - 6)]

  =  (1/2)[(27 - 9) - (18)]

  =  (1/2)(18 - 18)

  =  0

Hence the given points are collinear.

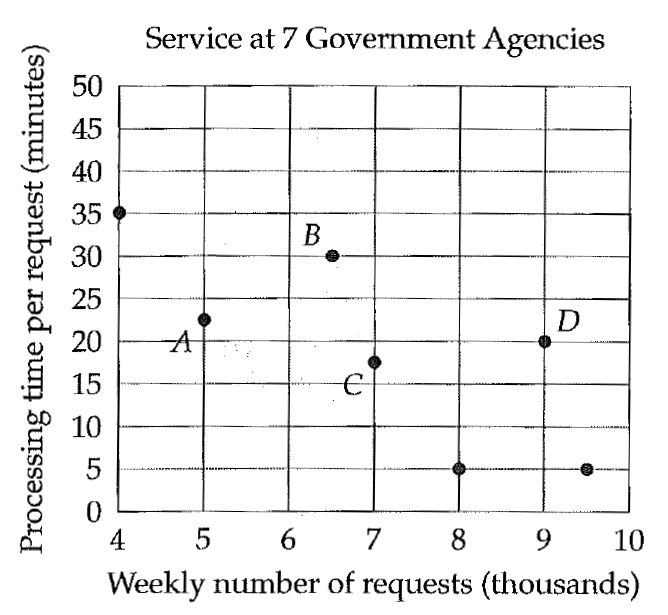
4. 4) In each of the following, find the value of k for which the given points are collinear.

(i) (k, -1)  ( 2, 1) and (4, 5)

Solution :

If the given points are collinear then the area of triangle is zero

(1/2) [(k + 10 – 4) – (-2 + 4 + 5k)] = 0

[(k + 6) – (2+ 5k)] = 0 x 2

(k + 6 – 2 - 5k) = 0

-4 k + 4 = 0

     - 4k = -4

         K = (-4)/(-4)

         K = 1

Hence, the value of k is 1

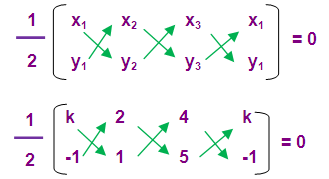
(ii) (2, -5)  ( 3, -4) and (9, k)

Solution :

If the given points are collinear then the area of triangle is zero

(1/2) [(-8 + 3k – 45) – (-15 - 36 + 2k)]  =  0

[(3k - 53) – (-51+ 2k)]  =  0 x 2

(3k - 53 + 51- 2k)  =  0

 k - 2  =  0

k  =  2

Hence the value of k is 2

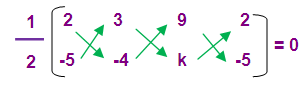
(iii) (k, k)  (2, 3) and (4, -1)

Solution :

If the given points are collinear then the area of triangle is zero

(1/2) [(3k - 2 + 4k) – (2k + 12 - k)]  =  0

[(7k - 2) – (k+12)]  =  0 x 2

(7k - 2 – k - 12)  =  0

 6 k - 14  =  0

6k  =  14

K  =  14/6  

K  = 7/3

Hence the value of k is 7/3.

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.