FINDING AREA OF TRIANGLES WITH THREE VERTICES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
If the three points (h, 0)
(a, b) and (0, k) lie on a straight line, then using the area of the triangle
formula show that (a/h) + (b/k) = 1, where h, k ≠ 0
Solution :
Let A(h, 0) B (a, b) and C (0, k) are the three points
Since the three points A (h, 0) B (a, b) and C (0, k) lie on a straight line we can say that the three points are collinear
So , area of triangle ABC = 0
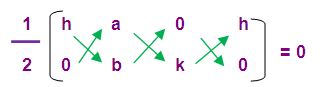
(1/2) [ (h b + a k + 0) – (0 + 0 + kh) ] = 0
[ h b + a k – k h ] = 0 x 2
h b + a k - k h = 0
h b + a k = k h
Divided (k h) on both sides,
(h b)/(k h) + (a k)/(k h) = (k h)/(k h)
(b/k) + (a/h) = 1
(a/h) + (b/k) = 1
Problem 2 :
Find the area of the triangle formed by joining the midpoints of the sides of a triangle whose vertices are (0, -1) (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.
Solution :
Let A (0,-1) B (2,1) and C (0,3) are the vertices of the triangle. D,E and F are the midpoints of the side AB,BC and CA respectively.
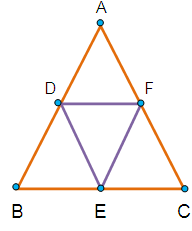
Midpoint of AB = (x1 + x2)/2 , (y1 + y2)/2
= (0 + 2)/2 , (-1 + 1)/2
= 2/2 , 0/2
= D (1,0)
Midpoint of BC = (x1 + x2)/2 , (y1 + y2)/2
= (2 + 0)/2 , (1 + 3)/2
= 2/2 , 4/2
= E (1,2)
Midpoint of CA = (x1+x2)/2 , (y1+y2)/2
= (0 + 0)/2 , (3 + (-1))/2
= 0/2 , 2/2
= F (0,1)
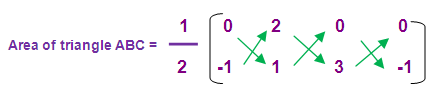
= (1/2) [(0 + 6 + 0) – (-2 + 0 + 0)]
= (1/2) [6+2]
= (1/2) [8]
= 4 square units

= (1/2) [(2 + 1 + 0) – (0 + 0 + 1)]
= (1/2) [3-1]
= (1/2) [2]
= 1 square units
Area of triangle ABC: Area of triangle DEF
4 : 1
Problem 3 :
If the points A(-3, 9), B (a, b) and C(4, -5) are collinear and if a + b = 1, then find a and b.
Solution :
Since these point are collinear,
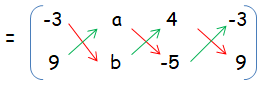
(-3b - 5a + 36) - (9a + 4b + 15) = 0
-3b - 5a + 36 - 9a - 4b - 15 = 0
-14a - 7b + 21 = 0
Dividing by 7, we get
-2a - b + 3 = 0
-2a - b = -3
2a + b = 3 --------(1)
Given that a + b = 1 --------(2)
(1) - (2)
2a + b - a - b = 3 - 1
a = 2
Applying the value of a, we get
2(2) + b = 3
4 + b = 3
b = 3 - 4
b = -1
So, the values of a and b are 2 and -1 respectively.
Problem 4 :
The area of a triangle is 5 sq.units. Two of its vertices are (2, 1) and (3, –2). The third vertex is (x, y) where
y = x + 3
Find the coordinates of the third vertex.
Solution :
Area of the triangle formed by by the above vertices
= 5 square units
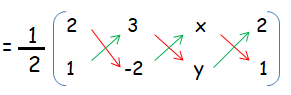
(1/2) [(-4 + 3y + x) - (3 - 2x + 2y)] = 5
[-4 + 3y + x - 3 + 2x - 2y] = 10
3x + y - 7 = 10
3x + y = 17 ----(1)
y = x + 3 ----(2)
Applying the value of y in (1), we get
3x + x + 3 = 17
4x = 17 - 3
4x = 14
x = 14/4
x = 3.5
Problem 5 :
Find the area of a triangle formed by the lines 3x + y - 2 = 0, 5x + 2y - 3 = 0 and 2x - y - 3 = 0
Solution :
3x + y - 2 = 0 ----(1)
5x + 2y - 3 = 0 ------(2)
2x - y - 3 = 0 ------(3)
(1) ⋅ 2 - (2)
6x + 2y - 4 - (5x + 2y - 3) = 0
6x + 2y - 4 - 5x - 2y + 3 = 0
1x - 1 = 0
x = 1
Applying the value of x in (1), we get
3(1) + y - 2 = 0
3 + y - 2 = 0
1 + y = 0
y = -1
So, the point of intersection of (1) and (2) is (1, -1).
(2) + 2 ⋅ (3)
5x + 2y - 3 + 2(2x - y - 3) = 0
5x + 2y - 3 + 4x - 2y - 6 = 0
9x - 9 = 0
9x = 9
x = 1
Applying the value of x in (2), we get
5(1) + 2y - 3 = 0
5 + 2y - 3 = 0
2y + 2 = 0
2y = -2
y = -1
So, the point of intersection of (2) and (3) is (1, -1).
(1) + (3)
3x + y - 2 + 2x - y - 3 = 0
5x - 5 = 0
5x = 5
x = 5/5
x = 1
Applying the value of x n (1)
3(1) + y - 2 = 0
3 - 2 + y = 0
1 + y = 0
y = -1
So, the point of intersection of (1) and (3) is (1, -1).
Since all points are the same, these are collinear it may not create a triangle. Then its area will become 0.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact US | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
10 Hard SAT Math Questions (Part - 39)
Dec 11, 25 05:59 PM
10 Hard SAT Math Questions (Part - 39) -
10 Hard SAT Math Questions (Part - 38)
Dec 08, 25 12:12 AM
10 Hard SAT Math Questions (Part - 38) -
SAT Math Practice
Dec 05, 25 04:04 AM
SAT Math Practice - Different Topics - Concept - Formulas - Example problems with step by step explanation

