TRIANGLES WORKSHEET

Question 1 :

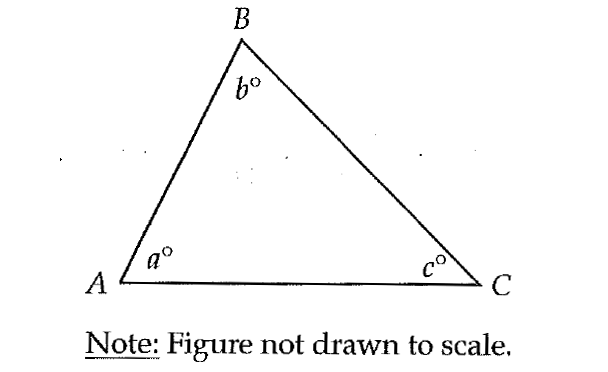
The triangle above is isosceles and b > a. Which of the following must be FALSE?

A) AB = BC

B) AB = AC

C) AC = BC

D) a = c

Question 2 :

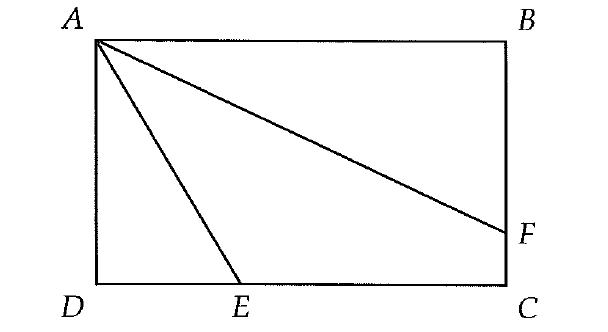
In rectangle ABCD above, E is on DC, F is on BC, DE = 6 and FC = 1. If angle A is trisected (divided into three equal angles) by AE and AF, what is the length of BF?

A) 5

B) 5√2 - 1

C) 5√3 - 1

D) 6√3 - 1

Question 3 :

In the figure above, AB = AC and c° = 50°. What is the value of a?

A) 65

B) 70

C) 75

D) 80

Question 4 :

The lengths of the sides of a triangle are different prime numbers. If two of the sides have lengths 3 and 11, which of the following could be the length of the third side?

I. 7

II. 13

III. 17

A) I only

B) II only

C) I and II only

D) I, II and III

Question 5 :

In the figure above, DE is parallel to AB. If AD = 6, DC = 3 and AB = 18, what is the length of DE?

Question 6 :

In the figure above, ∠BAC = 20° and AB = AC. If triangles ACD and ADE are isosceles, what is the value of x?

Question 7 :

Which of the following CANNOT be the lengths of the sides of a triangle?

A) 3, 5, 7

B) 3, 24, 24

C) 4, 6, 9

D) 4, 7, 2

Question 8 :

In the figure above, AB = BC and ∠ABC = 110°. What is the value of y?

Answers

1. Answer :

In the triangle shown above, b° > a°. So b° ≠ a°.

AC is the side corresponding to b° and BC is the side corresponding to a°.

Since b° ≠ a°,  AC ≠ BC.

But the answer choice (C) says that AC = BC.

So, (C) AC = BC must be FALSE.

The correct answer choice is (C).

2. Answer :

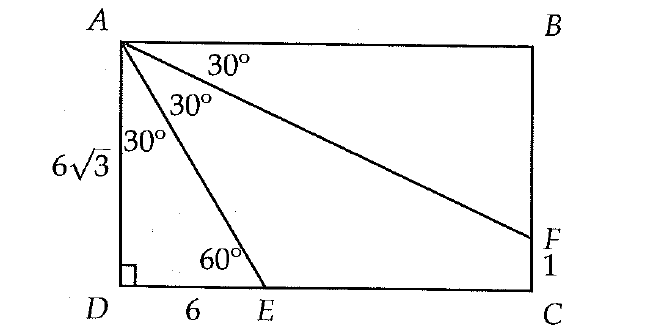
ΔADE is a 30° - 60° - 90° triangle.

DE is the shortest leg, because it is opposite to 30° and the next longer leg is AD which is opposite to 60° and the hypotenuse is AE.

In a 30° - 60° - 90° special right triangle, length of the of the shortest leg is always assumed to be 'x'.

Then, the lengths of other two legs in terms of 'x' :

Length of the longer leg = √3x

Length of the hypotenuse (AE) = 2x

So, the length of AD :

= √3(6)

= 6√3

In a rectangle, opposite sides are always equal in length.

Then,

BC = 6√3

BF + FC = 6√3

Substitute FC = 1.

BF + 1 = 6√3

Subtract 1 from both sides.

BF = 6√3 - 1

The correct answer choice is (D).

3. Answer :

In the triangle above, the angle measure corresponding to the leg AB is c° and the angle measure corresponding to the leg AC is b°.

Since AB = AC,

c° = b°

In ΔABc above,

a° + b° + c° = 180°

Since c° = b°, replace b° by c°.

a° + c° + c° = 180°

a + 2c = 180

Substitute c = 50.

a + 2(50) = 180

a + 100 = 180

Subtract 100 from both sides.

a = 80

The correct answer choice is (D).

4. Answer :

Key Concept : In any triangle, the sum of the lengths of any two sides must be greater than the length of third side.

I. 7 :

7 + 3 > 11  ✘

I. 7 does not work.

II. 13 :

13 + 3 > 11  ✔

13 + 11 > 3  ✔

3 + 11 < 13  ✔

II. 13 works in all the ways.

III. 17 :

17 + 3 > 11  ✔

17 + 11 > 3  ✔

3 + 11 > 17  ✘

III. 17 does not work.

The correct answer choice is (B).

5. Answer :

Since DE is parallel to AB, AC and BC are transversals.

∠BAC and ∠EDC are corresponding angles,

m∠BAC = m∠EDC

∠ABC and ∠DEC are corresponding angles,

m∠ABC = m∠DEC

Two angles of ΔABC are congruent to two angles of ΔDEC.

By Angle-Angle Similarity Theorem, ΔABC and ΔDEC are similar triangles Hence, the sides are proportional.

DE/AB = DC/AC

DE/18 = 3/9

Multiply both sides by 18.

DE = 6

6. Answer :

In ΔABC, the angle corresponding to the side AB is ∠ACB and the angle corresponding to the side AC is ∠ABC.

Since AB = AC,

∠ACB = ∠ABC

In ΔABC,

∠BAC + ∠ABC + ∠ACB = 180°

20° + ∠ABC + ∠ACB = 180°

20° + ∠ABC + ∠ACB = 180°

∠ABC + ∠ACB = 160°

∠ABC = ∠ACB = 80°

In the figure above, ∠ACB and ∠ACD together form a linear pair.

∠ACB + ∠ACD = 180°

80° + ∠ACD = 180°

∠ACD = 100°

Given : ΔACD is an isosceles triangle.

So, two of its angles must be equal.

Since ∠ACD = 100°, the remaining two angles ∠CAD and ∠ADC must be equal.

In ΔACD,

∠ACD + ∠CAD + ∠ADC = 180°

100° + ∠CAD + ∠ADC = 180°

∠CAD + ∠ADC = 80°

∠CAD = ∠ADC = 40°

In the figure above, ∠ADC and ∠ADE together form a linear pair.

∠ADC + ∠ADE = 180°

40° + ∠ADE = 180°

∠ADE = 140°

Given : ΔADE is an isosceles triangle.

So, two of its angles must be equal.

Since ∠ADE = 140°, the remaining two angles ∠AED and ∠DAE must be equal.

In ΔADE,

∠ADE + ∠AED + ∠DAE = 180°

140° + ∠AED + ∠DAE = 180°

∠AED + ∠DAE = 40°

∠AED = ∠DAE = 20°

Given : ∠AED = x°.

Therefore,

x = 20

7. Answer :

Key Concept : In any triangle, the sum of the lengths of any two sides must be greater than the length of third side.

Choice (A) :

Given side lengths : 3, 5, 7.

3 + 5 > 7  ✔

5 + 7 > 3  ✔

3 + 7 > 5  ✔

3, 5, 7 can be the lengths of the sides of a triangle.

Choice (B) :

Given side lengths : 3, 24, 24.

3 + 24 > 24  ✔

24 + 24 > 3  ✔

3 + 24 > 24  ✔

3, 24, 24 can be the lengths of the sides of a triangle.

Choice (C) :

Given side lengths : 4, 6, 9.

4 + 6 > 9  ✔

6 + 9 > 4  ✔

4 + 9 > 6  ✔

4, 6, 9 can be the lengths of the sides of a triangle.

Choice (D) :

Given side lengths : 4, 7, 2.

4 + 7 > 2  ✔

7 + 2 > 4  ✔

4 + 2 > 7  ✘

4, 7, 2 CANNOT be the lengths of the sides of a triangle.

8. Answer :

In ΔABC, the angle corresponding to the side AB is ∠C and the angle corresponding to the side BC is ∠A.

Since AB = AC,

∠C = ∠A

In ΔABC,

∠A + ∠B + ∠C = 180°

∠A + 110° + ∠C = 180°

Subtract 110° from both sides.

∠A + ∠C = 70°

Since ∠C = ∠A and ∠A + ∠C = 70°,

∠A = ∠C = 35°

In the figure above, ∠C and y° together form a linear pair.

∠C + y° = 180°

35° + y° = 180°

y = 145

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.