TRIGONOMETRIC FUNCTIONS OF ANGLES GREATER THAN 360 DEGREES

In the trigonometric functions sin θ, cos θ, tan θ, csc θ, sec θ and cot θ, if the angle θ is greater than or equal to 360°, we have to do the following steps.

(i)  Divide the given angle by 360° and

(ii)  Take the remainder

For example, let us consider the angle 450°.

When we divide 450 by 360, we get the remainder 90. 

Therefore, 450° should be taken as 90°. 

Let us consider the angle 360°.

When we divide 360 by 360, we get the remainder 0.

Therefore, 360° should be taken as 0°. 

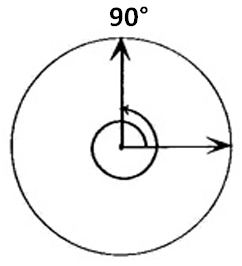
More clearly, 

450°  =  90° means, after having completed one circle of 360°, the position of the angle will be at 90°

It has been given in the figure given below. 

ASTC Formula

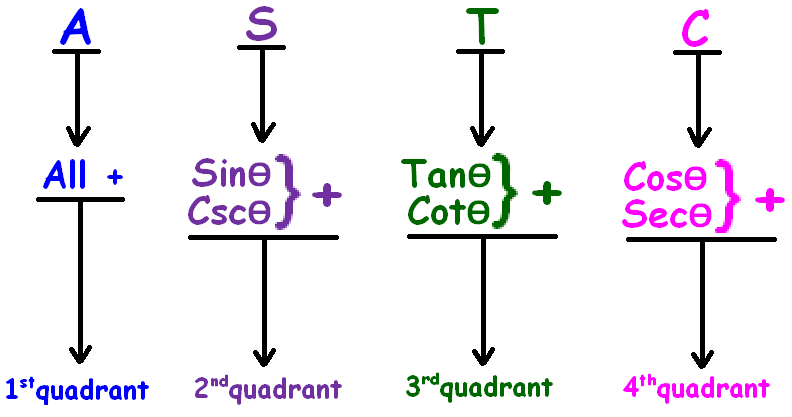
To know the sign of the value of trigonometric function, we have to be aware of ASTC formula.

The ASTC formula can be remembered easily using the following phrases.

"All Sliver Tea Cups" 

or

"All Students Take Calculus"

ASTC formula has been explained clearly in the figure shown below.

More clearly 

In the first quadrant (0° to 90°), all trigonometric ratios are positive.

In the second quadrant (90° to 180°), sin and csc are positive and other trigonometric ratios are negative.

In the third quadrant (180° to 270°), tan and cot are positive and other trigonometric ratios are negative.

In the fourth quadrant (270° to 360°), cos and sec are positive and other trigonometric ratios are negative.

Important Conversions

When we have the angles 90° and 270° in the trigonometric ratios in the form of

(90° + θ)

(90° - θ)

(270° + θ)

(270° - θ)

We have to do the following conversions, 

sin θ <------> cos θ

tan θ <------> cot θ

csc θ <------> sec θ

For example,

sin (270° + θ)  =  - cos θ

cos (90° - θ)  =  sin θ

For the angles 0° or 360° and  180°, we should not make the above conversions. 

Division of Quadrants 

(90° - θ) -------> I st Quadrant

(90° + θ) and (180° - θ) -------> II nd Quadrant

(180° + θ) and (270° - θ) -------> III rd Quadrant

(270° + θ), (360° - θ) and (- θ) -------> IV th Quadrant

Practice Problems

Problem 1 :

Evaluate tan 765°.

Solution : 

The given 765° is greater than 360°.

So, we have to divide 765 by 360 and take the remainder. 

When 765 is divided by 360, the remainder is 45. 

Therefore,

765°  =  45°

Then,

tan 765°  =  tan 45°

tan 765°  =  1

Problem 2 :

Evaluate cos (-870°).

Solution : 

Since the given angle (-870°) has negative sign, we have to assume it falls in the fourth quadrant.

In the fourth quadrant, "cos" is positive. 

So, we have cos (-870°)  =  cos 870°.

The given 870° is greater than 360°.

So, we have to divide 870 by 360 and take the remainder. 

When 870 is divided by 360, the remainder is 150. 

Therefore,

870°  =  150°

Then,

cos 870°  =  cos 150° 

cos 870°  =  cos (180° - 30°)

cos 870°  =  - cos 30°

cos 870  =  - √3/2

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.