HOW TO FIND VALUES OF TRIGONOMETRIC FUNCTIONS OF ANY ANGLE

The following steps will be useful to find the value of trigonometric functions for any angle.

Step 1 :

To find the value of any trigonometric angles, first we have to write the given angles in any one of the following forms.

Note :

If the given angle measures more than 360 degree, we have to divide it by 360 and write the remainder in one of the above forms.

Step 2 :

If we write the given angles in the form (90 + θ), (90 - θ), (270 + θ) or (270 - θ), we have to convert the given trigonometric ratios as follows.

sin θ  <---> cos θ

cosec θ  <---> sec θ

tan θ  <---> cot θ

Note :

We have a advantage for cos and sec functions.

That is,

cos ( - θ)  =  cos θ     and    sec (-θ)  =  sec θ

But for other trigonometric ratios,

Values of Trigonometric Angles

Practice Problems

Problem 1 :

Find the value of sin 480°.

Solution :

sin 480° =  sin 120°   =  sin (90 + 30) =  cos 30 120° lies in 2nd quadrant. For sin and cosec, we will have positive  =  √3/2

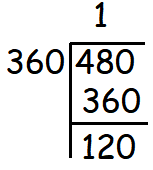So, the value of sin 480° is √3/2.

Problem 2 :

Find the value of sin (-1110°).

Solution :

sin (-1110°)  =  -sin 1110°   =  -sin 30 30° lies in 1st quadrant. For all trigonometric ratios, weh ave positive. =  -1/2

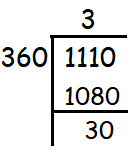So, the value of sin (-1110°) is -1/√2.

Problem 3 :

Find the value of cos 300°.

Solution :

 cos 300°  =  cos (270 + 30)

300° lies in 4^th quadrant. For cos and sec, we will have positive.

   =  sin 30

  =  1/2

So, the value of cos 300° is 1/2.

Problem 4 :

Find the value of tan 1050°.

Solution :

tan 1050°  =  tan 330   =  tan (270 + 60) =  -cot 60 300° lies in 4th quadrant. For cos and sec, we will have positive. =  -1/√3

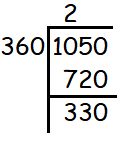So, the value of tan 1050° is  -1/√3.

Problem 4 :

Find the value of cot 660°.

Solution :

tan 660°  =  tan 300   =  tan (270 + 30) =  -cot 30 300° lies in 4th quadrant. For cos and sec, we will have positive. =  -√3

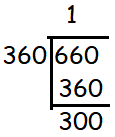So, the value of cot 660° is -√3.

Problem 4 :

Find the value of cot 19π/3.

Solution :

cot 19π/3  =  cot (6π + π/3)

  =  cot  π/3

=  √3

Problem 4 :

Find the value of sin (-11π/3).

Solution :

sin (-11π/3)  =  -sin (4π - π/3)

  =  sin π/3

=  √3/2

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.