TRIGONOMETRIC IDENTITIES EXAMPLES

Abbreviations used :

L.H.S -----> Left hand side

R.H.S -----> Right hand side

Example 1 : 

Prove :

tanθ/(1 - tan²θ)  =  sinθsin(90 - θ)/[2sin²(90 - θ) - 1]

Solution :

L.H.S

   =  tan θ/(1 - tan²θ)

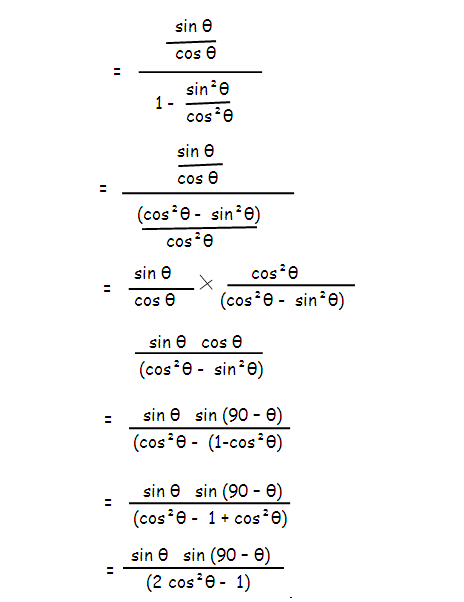
  =  sinθsin(90 - θ)/[2sin²(90 - θ) - 1]

=  R.H.S

Example 2 : 

Prove :

[1/(cosecθ - cotθ)] - (1/sinθ) 

=  [(1/sinθ)] - [1/(cosecθ + cotθ)]

Solution :

L.H.S :

=  [1/(cosecθ - cotθ)] - (1/sinθ)

Multiply numerator and denominator of the first fraction by (cosecθ + cotθ).

=  [(1/(cosecθ - cotθ)) x (cosecθ + cotθ)/(cosecθ + cotθ)] - (1/sinθ)

=  (cosecθ  + cotθ)/(cosec²θ - cot²θ) - (1/sinθ)

=  [(cosecθ + cotθ)/1] - (1/sinθ)

=  [(cosecθ + cotθ) - cosecθ]

=  cotθ -----(1)

R.H.S :

=  (1/sinθ) - [1/(cosecθ - cotθ)]

Multiply the numerator and denominator of the second fraction by (cosecθ + cotθ).

=  [(cosecθ - cotθ)/(cosecθ - cotθ)(cosecθ + cotθ)] - (1/sinθ)

=  (cosecθ + cotθ)/(cosec²θ - cot²θ) - (1/sinθ)

   =  [(cosecθ + cotθ)/1] - (1/sinθ)

   =  [(cosecθ + cotθ) - cosecθ]

   =  cotθ -----(2)

From (1) and (2), we get

L.H.S  =  R.H.S

Example 3 : 

Prove :

(cot²θ + sec²θ) / (tan²θ +  cosec²θ) 

=  sinθcosθ(tanθ + cotθ)

Solution :

L.H.S :

=  (cot²θ + sec²θ)/(tan²θ + cosec²θ)

=  (cosec²θ - 1 + 1 + tan²θ)/(tan²θ + cosec²θ)

=  (tan²θ + cosec²θ)/(tan²θ + cosec²θ)

=  1 -----(1)

R.H.S :

=  sinθcosθ(tanθ + cotθ)

=  sinθcosθ[(sinθ/cosθ) + (cosθ/sinθ)]

=  sinθcosθ[(sin²θ + cos²θ)/(cosθsinθ)]

  =  sinθcosθ [1/(cosθsinθ)]

=  1 -----(2)

From (1) and (2), we get

L.H.S  =  R.H.S

Example 4 :

If x = asecθ + btanθ and y = atanθ + bsecθ then prove that

x² - y²  =  a² - b²

Solution :

x²  =  (asecθ + btanθ)²

x²  =  (asecθ)² + (btanθ)² + 2absecθtanθ

x²  =  a²sec²θ + b²tan²θ + 2absecθtanθ -----(1)

y²  =  (atanθ + bsecθ)²

y²  =  (atanθ)² + (bsecθ)² + 2abtanθsecθ

y²  =  a²tan²θ + b²sec²θ + 2abtanθsecθ -----(2)

(1) - (2) :

x² - y²  =  (a²sec²θ + b²tan²θ + 2absecθtanθ)

- (a²tan²θ + b²sec²θ + 2abtanθsecθ)

x² - y²  =  a²sec²θ + b²tan²θ + 2absecθtanθ

- a²tan²θ - b²sec²θ - 2abtanθsecθ

x² - y²  =  a²sec²θ + b²tan²θ - a²tan²θ - b²sec²θ

x² - y²  =  a²sec²θ - a²tan²θ - b²sec²θ + b²tan²θ

x² - y²  =  a²(sec²θ - tan²θ) - b²(sec²θ - tan²θ)

x² - y²  =  a²(1) - b²(1)

x² - y²  =  a² - b²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.