TRIGONOMETRIC LIMITS PROBLEMS AND SOLUTIONS

Problem 1 :

Evaluate the following limit 

lim _{x-> 0}  (1 + sin x)^{2 cosec x}

Solution :

  =  lim _{x-> 0}  (1 + sin x)^{2 cosec x}

Let y = sin x

If x -> 0, then y -> 0

cosec x  =  1/ sin x  =  1/y

lim _{x-> 0}  (1 + sin x)^{2 cosec x}  =  lim _{x-> 0}  (1 + y)^2/y

 lim _{x-> 0}  (1 + x)^1/x  =  e

  =  e²

Problem 2 :

Evaluate the following limit 

 lim _{x-> 0} (√2 - √(1 + cos x)) / sin² x

Solution :

  =  lim _{x-> 0}  (√2 - √(1 + cos x)) / sin² x

By applying the limit value directly in the given question, we get 0/0. That is indeterminate form.

So let us rationalize the numerator,

  =  lim_x->0((√2-√(1+cosx))/sin²x)⋅[(√2+√(1+cosx))/(√2+√(1+ cosx))]

  =  lim_x->0((2-(1+cosx))/sin²x(√2+√(1+ cosx))

  =  lim_x->0 (1-cosx)/[1+cosx)(1-cosx)(√2+√(1+ cosx))]

  =  lim_x->0 1/[(1+cosx)(√2+√(1+ cosx))]

  =  1/[2(√2+√(1+1)]

  =  1/4√2

Hence the value of  lim _{x-> 0} (√2 - √(1 + cos x)) / sin² x is 1/4√2.

Problem 3 :

Evaluate the following limit 

 lim _{x-> 0} (√(1+sinx) - √(1-sinx)) / tan x

Solution :

  =   lim _{x-> 0} (√(1+sinx) - √(1-sinx)) / tan x

By rationalizing the numerator, we get

  =   lim _{x-> 0} (1+sinx) - (1-sinx)/tan x(√(1+sinx)+√(1-sinx))

  =   lim _{x-> 0} 2sinx/tan x(√(1+sinx)+√(1-sinx))

tan x =  sin x/cos x

  =   lim _{x-> 0} 2 cos x/(√(1+sinx)+√(1-sinx))

By applying the limit, we get

  =   2 /2

  =  1

Hence the value of  lim _{x-> 0} (√(1+sinx) - √(1-sinx)) / tan x is 1.

Problem 4 :

Evaluate the following limit

lim _{x-> ∞}  {(x² – 2x + 1)/(x²-4x+2))^x

Solution :

  =  lim _{x-> ∞}  {(x² – 2x + 1)/(x²-4x+2))^x

By applying the limit value directly in the given question, we get indeterminant form.

  =  lim _{x-> ∞}  {(x² – 2x + 1)/(x²-4x+2))^x

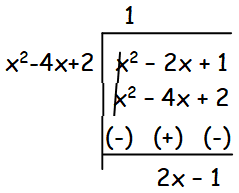
  =  lim _{x-> ∞}  {1 + ((2x - 1)/(x²-4x+2))^x}

  =  lim _{x-> ∞}  {1 + ((2x - 1)/(x²-4x+2))

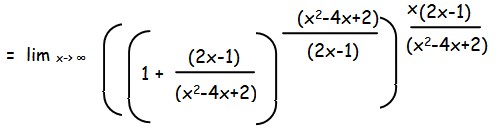
Let y = (2x- 1)/(x²-4x+2)

If x -> ∞, then y =  xx(2- 1/x)/x²(1-4/x+2/x²), y -> 2

  =  lim _{y-> 0} {(1 + y)^1/y}^y

  =  e^y

By applying the value of y, we get

  =  e²

Hence the value of lim _{x-> ∞}  {(x² – 2x + 1)/(x²-4x+2))^x is e²

Problem 5 :

Evaluate the following limit

lim _{x-> 0}  (e^x - e^-x) / sin x

Solution :

  =  lim _{x-> 0}  (e^x - e^-x) / sin x

  =  lim _{x-> 0}  (e^x - (1/e^x)) / sin x

  =  lim _{x-> 0}  ((e^x)² - 1)/e^x sin x

  =  lim _{x-> 0}  (e^2x - 1)/e^x sin x

Now we are going to multiply numerator by 2x/2x, sin x by (x/x)

  =  lim _{x-> 0}  (e^2x - 1)(2x/2x)/e^x sin x (x/x)

  =  lim _{x-> 0}  ((e^2x - 1)/2x)(2x/x)/(e^x (sin x/x))

  =  2lim _{x-> 0} ((e^2x - 1)/2x)/lim _{x-> 0}(e^x lim _{x-> 0}(sin x/x))

  =  2(1)/1(1)

  =  2

Hence the value of lim _{x-> 0}  (e^x - e^-x) / sin x is 2.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.