TRIGONOMETRIC RATIOS OF COMPOUND ANGLES

An angle made up of the algebraic sum of two or more angles is called a compound angle.

Formulas for trigonometric ratios of compound angles : 

sin(A + B) = sinAcosB + cosAsinB

sin(A - B) = sinAcosB - cosAsinB

cos(A + B) = cosAcosB - sinAcosB

cos(A - B) = cosAcosB + sinAcosB

tan(A + B) = (tanA + tanB)/(1 - tanAtanB)

tan(A - B) = (tanA - tanB)/(1 + tanAtanB)

Trigonometric Ratio Table

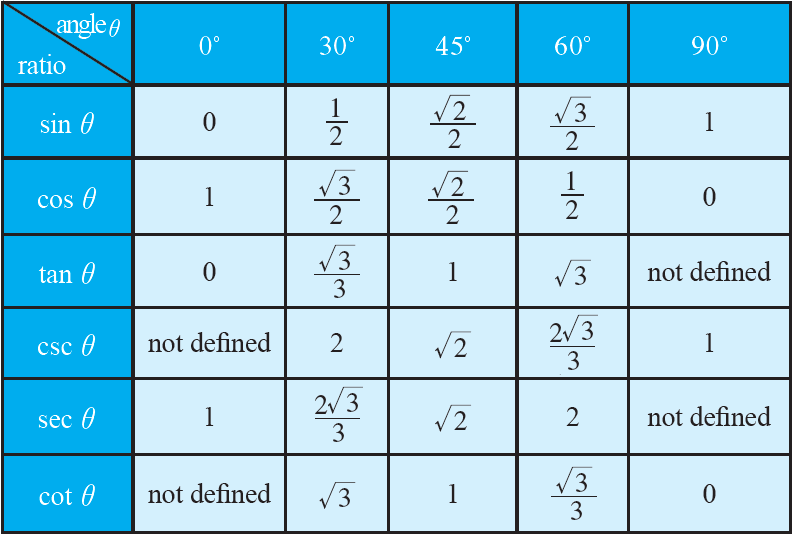
From the above table, we can get the values of trigonometric ratios for standard angles such as 0°, 30°, 45°, 60°, 90°.

Solved Problems

Problem 1 :

Find the value of cos15°.

Solution :

Write the given angle 15° in terms of sum or difference of two standard angles. 

15° = 45° - 30°

cos15° = cos(45° - 30°)

= cos45°cos30° + sin45°sin30°

Using the above trigonometric ratio table, we have

= (√2/2) ⋅ (√3/2) + (√2/2) ⋅ (1/2)

= (√6/4)  +  (√2/4)

= (√6 + √2)/4

Problem 2 :

Find the value of cos105°.

Solution :

Write the given angle 105° in terms of  sum or difference of two standard angles. 

105° = 60° + 45°

cos105° = cos(60° + 45°)

= cos60°cos45° - sin60°sin45°

Using the above trigonometric ratio table, we have

= (1/2) ⋅ (√2/2) - (√3/2) ⋅ (√2/2)

= (√2/4)  -  (√6/4)

= (√2 - √6)/4

Problem 3 :

Find the value of sin75°.

Solution :

Write the given angle 75° in terms of  sum or difference of two standard angles. 

75° = 45° + 30°

sin75° = sin(45° + 30°)

= sin45°cos30° + cos45°sin30°

Using the above trigonometric ratio table, we have

= (√2/2) ⋅ (√3/2) + (√2/2) ⋅ (1/2)

= (√6/4) + (√2/4)

= (√6 + √2)/4

Problem 4 :

Find the value of tan15°.

Solution :

Write the given angle 15° in terms of  sum or difference of two standard angles. 

15° = 45° - 30°

tan15° = tan(45° - 30°)

= (tan45° -  tan30°)/(1 + tan45°tan30°)

Using the above trigonometric ratio table, we have

= (1 - 1/√3)/(1 + 1 ⋅ 1/√3)

=  (1 - 1/√3)/(1 + 1/√3)

= (√3/√3 - 1/√3)/(√3/√3 + 1/√3)

= [(√3 - 1)/√3]/[(√3 + 1)/√3]

= [(√3 - 1)/√3] x [(√3/(√3 + 1)]

= (√3 - 1)/(√3 + 1)

By rationalizing the denominator, we get 

= 2 - √3

Problem 5 :

If A and B are acute angles, sin A = 3/5, cos B = 12/13,  find cos (A + B). 

Solution :

cos(A + B) = cosAcosB - sinAsinB ----(1) 

To find the value of cos(A + B), we need the values of

cosA, cosB, sinA, sinB

The values of sinA and cos A are given in the question itself.

So, we have to find the value of sin B and cos A.

Finding the value of sin B : 

sin²B = 1 - cos²B

= 1 - (12/13)²

= 1 - 144/169

= (169 - 144)/169

= 25/169

sin²B = (5/13)²

sinB = 5/13

Finding the value of cos A :

cos²A = 1 - sin²A

= 1 - (3/5)²

= 1 - 9/25

= (25 - 9)/25

= 16/25

cos²A = (4/5)²

cos A = 4/5 

Substitute the values of cosA, cosB, sinA and sinB in (1).

(1)-----> cos(A + B) = (4/5) ⋅ (12/13) - (3/5) ⋅ (5/13)

= (4/5) ⋅ (12/13) - (3/5) ⋅ (5/13)

= (48/65) - (15/65)

= (48 - 15)/65

= 33/65

Compound Angles without Standard Angles

As we have seen in the above examples, some angles can not be written in terms of sum or difference of two standard angles.

For example, 

Let us consider sin225°.

Here, 225° can not be written in terms of sum or difference of two standard angles.

All that we can do is, 225° can be written in terms sum or difference of two angles where one of the angles will be quadrantal angles such as 0°, 90°, 180°, 270°

So, sin 225° can be written as  

sin(180° + 45°)  or  sin(270° - 45°)

To evaluate sin(180° + 45°)  or  sin(270° - 45°), we have to know ASTC formula

ASTC formula has been explained clearly in the figure given below.   

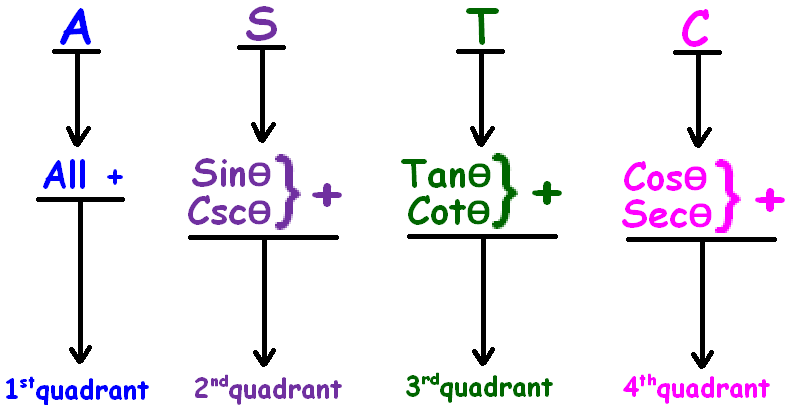
More clearly 

In the first quadrant (0° to 90°), all trigonometric ratios are positive.

In the second quadrant (90° to 180°), sin and csc are positive and other trigonometric ratios are negative.

In the third quadrant (180° to 270°), tan and cot are positive and other trigonometric ratios are negative.

In the fourth quadrant (270° to 360°), cos and sec are positive and other trigonometric ratios are negative.

Important Conversions

When we have the angles 90° and 270° in the trigonometric ratios in the form of

(90° + θ)

(90° - θ)

(270° + θ)

(270° - θ)

We have to do the following conversions, 

sinθ <----> cosθ

tanθ <----> cotθ

cscθ <----> secθ

For example,

sin(270° + θ) = - cosθ

cos(90° - θ) = sinθ

For the angles 0° or 360° and  180°, we should not make the above conversions. 

Evaluation of Trigonometric Ratios using ASTC Formula

Now, let us evaluate sin(180° + 45°).

To evaluate sin(90° + θ), we have to consider the following important points.

(i)  (180° + 45°) will fall in the III rd quadrant.

(ii)  When we have 180°, 'sin' will not be changed.

(iii)  In the III rd quadrant, the sign of 'sin' is negative.

Considering the above points, we have

sin225° = sin(180° + 45°)

sin225° = - sin45°

sin225° = - √2/2

When we are not able to write the given angle in terms of sum or difference of two standard angles, we have to proceed the problem in this way. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.