TRIGONOMETRIC RATIOS OF SOME SPECIFIC ANGLES

For certain specific angles such as 30°, 45° and 60°, which are frequently seen in applications, we can use geometry to determine the trigonometric ratios.

Trigonometric Ratios of 30° and 60°

Let ABC be an equilateral triangle whose sides have length a (see the figure given below). Draw AD perpendicular to BC, then D bisects the side BC.

Then,

BD  =  DC  =  a/2

∠BAD  =  ∠DAC  =  30°

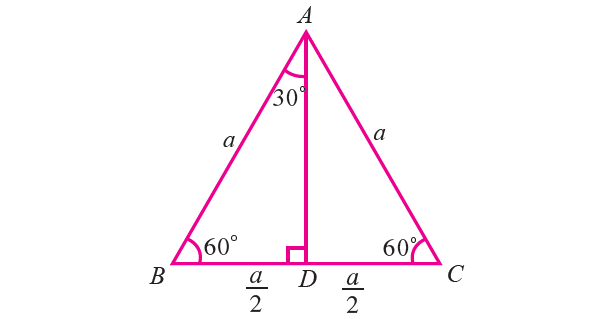
Now, in right triangle ADB, ∠BAD  =  30° and BD  =  a/2.

In right triangle ADB, by Pythagorean theorem, 

AB²  =  AD² + BD²

a²  =  AD² + (a/2)²

a² - (a²/4)  =  AD²

3a²/4  =  AD²

√(3a²/4)  =  AD

√3 ⋅ a/2  = m AD 

Hence, we can find the trigonometric ratios of angle 30° from the right triangle ADB. 

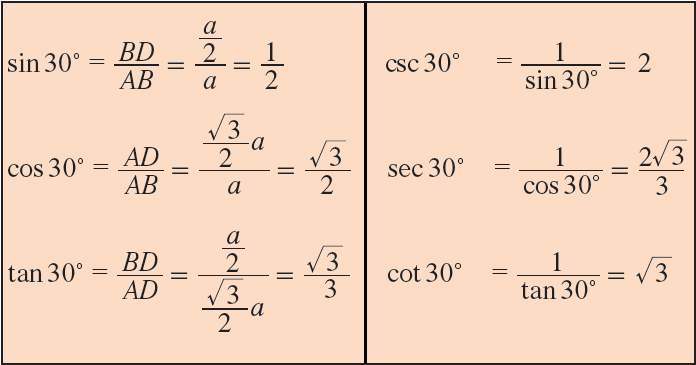
In right triangle ADB, ∠ABD  =  60°.

So, we can determine the trigonometric ratios of angle 60°. 

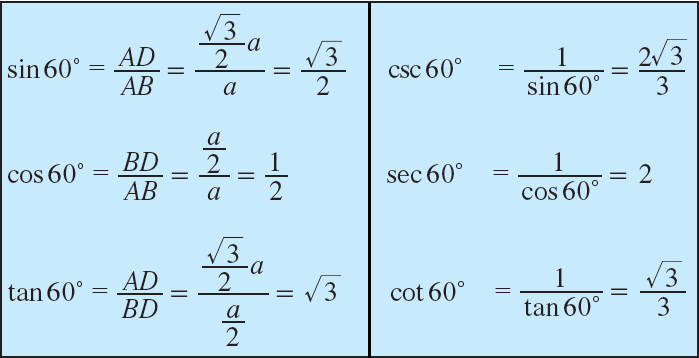
Trigonometric Ratio of 45°

If an acute angle of a right triangle is 45°, then the other acute angle is also 45°. 

Thus the triangle is isosceles. Let us consider the triangle ABC with 

∠B  =  90°

∠A  =  ∠C  =  45°

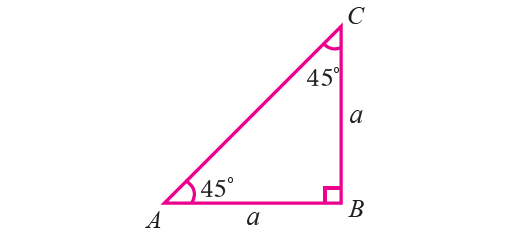
Then AB  =  BC.

Let AB  =  BC  =  a.

By Pythagorean theorem,

AC²  =  AB² + BC²

AC²  =  a² + a²

AC²  =  2a²

Take square root on each side.

AC  =  a√2

Hence, we can find the trigonometric ratios of angle 45° from the right triangle ABC. 

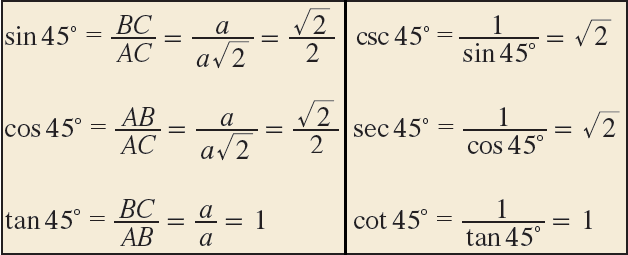
Trigonometric Ratios of 0° and 90°

Consider the figure given below which shows a circle of radius 1 unit centered at the origin.

Let P be a point on the circle in the first quadrant with coordinates (x, y).

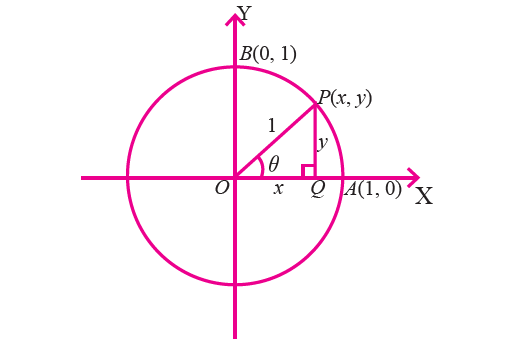
We drop a perpendicular PQ from P to the x-axis in order to form the right triangle OPQ.

Let ∠POQ  =  θ, then 

sin θ  =  PQ / OP  =  y/1  =  y  (y coordinate of P)

cos θ  =  OQ / OP  =  x/1  =  x  (x coordinate of P)

tan θ  =  PQ / OQ  =  y/x

If OP coincides with OA, then angle θ  =  0°.

Since, the coordinates of A are (1, 0), we have

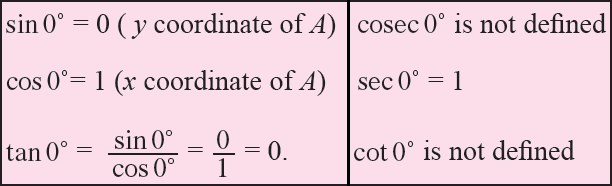
If OP coincides with OB, then angle θ  =  90°.

Since, the coordinates of B are (0, 1), we have

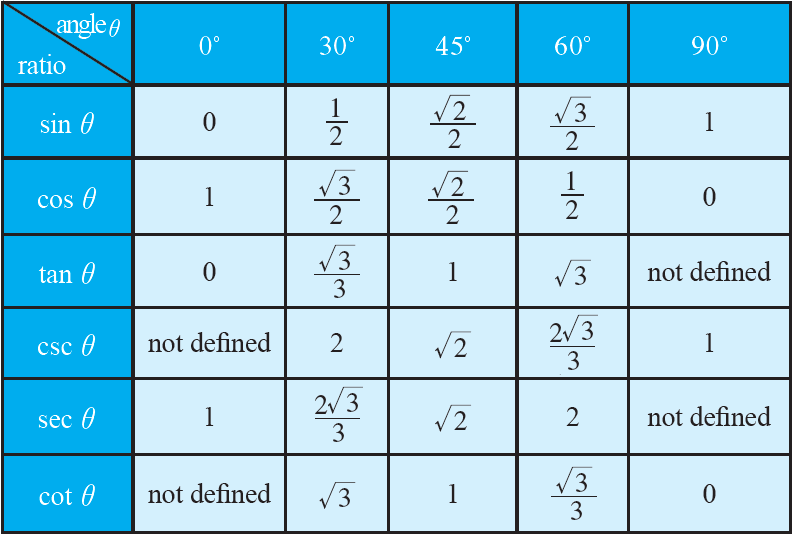
The six trigonometric ratios of angles 0°, 30°, 45°, 60° and 90° are provided in the following table.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.