TRIGONOMETRIC RATIOS OF SUPPLEMENTARY ANGLES

Two angles are supplementary to each other if their sum is equal to 180°.

Trigonometric-ratios of supplementary angles are given below.

Let us see, how the trigonometric ratios of supplementary angles are determined.

To know that, first we have to understand ASTC formula.

The ASTC formula can be remembered easily using the following phrases.

All Sliver Tea Cups

or

All Students Take Calculus

ASTC formula has been explained clearly in the figure given below.

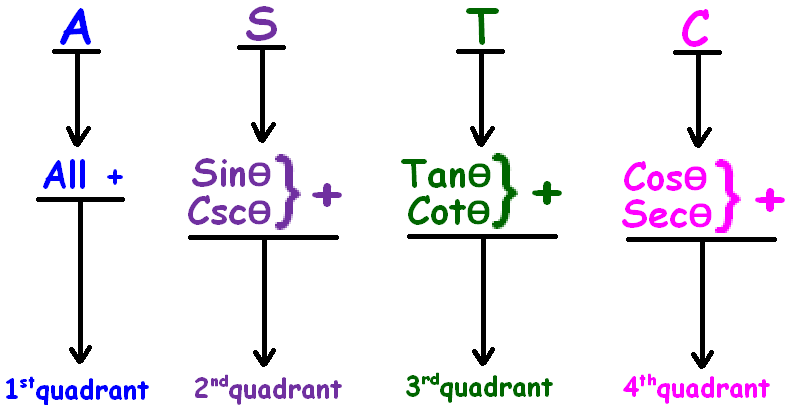
More clearly

From the above picture, it is very clear that

(i)  (180° - θ) falls in the second quadrant and

(i)  (180° + θ) falls in the third quadrant

In the second quadrant (180° - θ), sin and csc are positive and other trigonometric ratios are negative.

In the third quadrant (180° + θ), tan and cot are positive and other trigonometric ratios are negative.

Important Conversions

When we have the angles 90° and 270° in the trigonometric ratios in the form of

(90° + θ)

(90° - θ)

(270° + θ)

(270° - θ)

We have to do the following conversions,

sinθ <----> cosθ

tanθ <----> cotθ

cscθ <----> secθ

For example,

sin(270° + θ) = -cosθ

cos(90° - θ) = sinθ

For the angles 0° or 360° and  180°, we should not make the above conversions.

Evaluation of Trigonometric Ratios Using ASTC Formula

Example 1 :

Evaluate :

sin(180° - θ)

Solution :

To evaluate sin(180° - θ), we have to consider the following important points.

(i) (180° - θ) will fall in the II nd quadrant.

(ii) When we have 180°, "sin" will not be changed as "cos".

(iii) In the II nd quadrant, the sign of "sin" is positive.

Considering the above points, we have

sin(180° - θ) = sinθ

Example 2 :

Evaluate :

cos(180° - θ)

Solution :

To evaluate cos(180° - θ), we have to consider the following important points.

(i) (180° - θ) will fall in the II nd quadrant.

(ii) When we have 180°, "cos" will not be changed as "sin".

(iii) In the II nd quadrant, the sign of "cos" is negative.

Considering the above points, we have

cos(180° - θ) = -cosθ

Example 3 :

Evaluate :

tan(180° - θ)

Solution :

To evaluate tan(180° - θ), we have to consider the following important points.

(i) (180° - θ) will fall in the II nd quadrant.

(ii) When we have 180°, "tan" will not be changed as "cot".

(iii) In the II nd quadrant, the sign of "tan" is negative.

Considering the above points, we have

tan(180° - θ) = -tanθ

Example 4 :

Evaluate :

csc(180° - θ)

Solution :

To evaluate csc(180° - θ), we have to consider the following important points.

(i) (180° - θ) will fall in the II nd quadrant.

(ii) When we have 180°, "csc" will not be changed as "sec".

(iii) In the II nd quadrant, the sign of "csc" is positive.

Considering the above points, we have

csc(180° - θ) = cscθ

Example 5 :

Evaluate :

sec(180° - θ)

Solution :

To evaluate sec(180° - θ), we have to consider the following important points.

(i) (180° - θ) will fall in the II nd quadrant.

(ii) When we have 180°, "sec" will not be changed as "csc".

(iii) In the II nd quadrant, the sign of "sec" is negative.

Considering the above points, we have

sec(180° - θ) = -secθ

Example 6 :

Evaluate :

cot(180° - θ)

Solution :

To evaluate cot(180° - θ), we have to consider the following important points.

(i) (180° - θ) will fall in the II nd quadrant.

(ii) When we have 180°, "cot" will not be changed as "tan".

(iii) In the II nd quadrant, the sign of "cot" is negative.

Considering the above points, we have

cot(180° - θ) = -cotθ

Example 7 :

Evaluate :

sin(180° + θ)

Solution :

To evaluate sin(180° + θ), we have to consider the following important points.

(i) (180° + θ) will fall in the III rd quadrant.

(ii) When we have 180°, "sin" will not be changed as "cos".

(iii) In the III rd quadrant, the sign of "sin" is negative.

Considering the above points, we have

sin(180° + θ) = -sinθ

Example 8 :

Evaluate :

cos(180° + θ)

Solution :

To evaluate cos(180° + θ), we have to consider the following important points.

(i) (180° + θ) will fall in the III rd quadrant.

(ii) When we have 180°, "cos" will not be changed as "sin".

(iii) In the III rd quadrant, the sign of "cos" is negative.

Considering the above points, we have

cos(180° + θ) = -cosθ

Example 9 :

Evaluate :

tan(180° + θ)

Solution :

To evaluate tan(180° + θ), we have to consider the following important points.

(i) (180° + θ) will fall in the III rd quadrant.

(ii) When we have 180°, "tan" will not be changed as "cot".

(iii) In the III rd quadrant, the sign of "tan" is positive.

Considering the above points, we have

tan(180° + θ) = tanθ

Example 10 :

Evaluate :

csc(180° + θ)

Solution :

To evaluate csc(180° + θ), we have to consider the following important points.

(i) (180° + θ) will fall in the III rd quadrant.

(ii) When we have 180°, "csc" will not be changed as "sec".

(iii) In the III rd quadrant, the sign of "csc" is negative.

Considering the above points, we have

csc(180° + θ) = -cscθ

Example 11 :

Evaluate :

sec(180° + θ)

Solution :

To evaluate sec(180° + θ), we have to consider the following important points.

(i) (180° + θ) will fall in the III rd quadrant.

(ii) When we have 180°, "sec" will not be changed as "csc".

(iii) In the III rd quadrant, the sign of "sec" is negative.

Considering the above points, we have

sec(180° + θ) = -secθ

Example 12 :

Evaluate :

cot(180° + θ)

Solution :

To evaluate cot(180° + θ), we have to consider the following important points.

(i) (180° + θ) will fall in the III rd quadrant.

(ii) When we have 180°, "cot" will not be changed as "tan".

(iii) In the III rd quadrant, the sign of "cot" is positive.

Considering the above points, we have

cot(180° + θ) = cotθ

Summary (Supplementary Angles)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.